
【题目】已知数列{an}满足an+1= ![]() ,a1=1,n∈N* .
,a1=1,n∈N* .
(1)求a2 , a3 , a4的值;
(2)求数列{an}的通项公式.
【答案】
(1)解:∵数列{an}满足an+1= ![]() ,a1=1,n∈N*.∴a2=
,a1=1,n∈N*.∴a2= ![]() =
= ![]() ,同理可得:a3=
,同理可得:a3= ![]() ,a4=
,a4= ![]() .
.
(2)解:数列{an}满足an+1= ![]() ,a1=1,n∈N*.
,a1=1,n∈N*.
两边取倒数可得: ![]() =
= ![]() +
+ ![]() ,即
,即 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴数列 ![]() 是等差数列,首项为1,公差为
是等差数列,首项为1,公差为 ![]() ,
,
∴ ![]() =1+
=1+ ![]() (n﹣1),解得an=
(n﹣1),解得an= ![]() ,
,
∴an= ![]()
【解析】(1)由数列{an}满足an+1= ![]() ,a1=1,n∈N* . 分别令n=1,2,3,即可得出.(2)数列{an}满足an+1=
,a1=1,n∈N* . 分别令n=1,2,3,即可得出.(2)数列{an}满足an+1= ![]() ,a1=1,n∈N* . 两边取倒数可得:
,a1=1,n∈N* . 两边取倒数可得: ![]() ﹣
﹣ ![]() =
= ![]() ,再利用等差数列的通项公式即可得出.
,再利用等差数列的通项公式即可得出.
【考点精析】利用数列的通项公式对题目进行判断即可得到答案,需要熟知如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断其真假:
(1)p:不论m取何实数,方程x2+x-m=0必有实数根;
(2)q:存在一个实数x,使得x2+x+1≤0;
(3)r:等圆的面积相等,周长相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
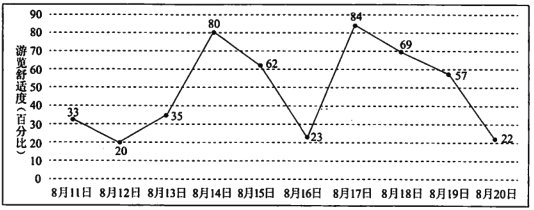
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨
产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨![]() 产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果
产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果![]() 产品的利润为300元/吨,
产品的利润为300元/吨, ![]() 产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
A. 14000元 B. 16000元 C. 18000元 D. 20000元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天100颗种子浸泡后的发芽数,得到如下资料:
K日 日期期 | 1日 | 2日 | 3日 | 4日 | 5日 |
温差x(℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
(1)求这5天发芽数的中位数;
(2)求这5天的平均发芽率;
(3)从3月1日至3月5日中任选2天,记前面一天发芽的种子数为m,后面一天发芽的种子数为n,用(m,n)的形式列出所有基本事件,并求满足“![]() ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com