
【题目】某学校为了学生的健康,对课间操活动做了如下规定:课间操时间若有雾霾则停止课间操,若无雾霾则组织课间操.预报得知,在未来一周从周一到周五的课间操时间出现雾霾的概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,且每一天出现雾霾与否是相互独立的.
,且每一天出现雾霾与否是相互独立的.
(1)求未来5天至少一天停止课间操的概率;
(2)求未来5天组织课间操的天数X的分布列和数学期望.
【答案】(1)![]() .(2)见解析,数学期望为2.
.(2)见解析,数学期望为2.
【解析】
(1)可以求出五天都可以出操的概率,然后用对立事件概率公式计算;
(2)天数X的可能取值为0,1,2,3,4,5,分别计算概率得分布列,由分布列可计算期望.
(1)课间操时间若有雾霾则停止课间操,若无雾霾则组织课间操.
预报得知,在未来一周从周一到周五的课间操时间出现雾霾的概率是:
前3天均为![]() ,后2天均为
,后2天均为![]() ,且每一天出现雾霾与否是相互独立的.
,且每一天出现雾霾与否是相互独立的.
∴未来5天每天都组织课间操的概率为:
P1![]() ,
,
∴未来5天至少一天停止课间操的概率:
P=1﹣P1=1![]() .
.
(2)未来5天组织课间操的天数X的可能取值为0,1,2,3,4,5,
P(X=0)![]() ,
,
P(X=1)![]() ,
,
P(X=2)![]() ,
,
P(X=3)![]() ,
,
P(X=4)![]() ,
,
P(X=5)![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
数学期望E(X)![]() 2.
2.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,称
,称![]() (其中
(其中![]() )为数列
)为数列![]() 的前k项“波动均值”.若对任意的
的前k项“波动均值”.若对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“趋稳数列”.
为“趋稳数列”.
(1)若数列1,![]() ,2为“趋稳数列”,求
,2为“趋稳数列”,求![]() 的取值范围;
的取值范围;
(2)若各项均为正数的等比数列![]() 的公比
的公比![]() ,求证:
,求证:![]() 是“趋稳数列”;
是“趋稳数列”;
(3)已知数列![]() 的首项为1,各项均为整数,前
的首项为1,各项均为整数,前![]() 项的和为
项的和为![]() . 且对任意
. 且对任意![]() ,都有
,都有![]() , 试计算:
, 试计算:![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
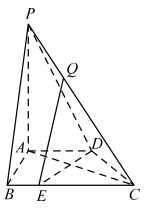
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,其中A,B是两个确定的实数,
,其中A,B是两个确定的实数,![]()
(1)若![]() ,求
,求![]() 的前n项和;
的前n项和;
(2)证明:![]() 不是等比数列;
不是等比数列;
(3)若![]() ,数列
,数列![]() 中除去开始的两项外,是否还有相等的两项,并证明你的结论.
中除去开始的两项外,是否还有相等的两项,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,四边形ACEF为正方形,且平面
,四边形ACEF为正方形,且平面![]() 平面ACEF.
平面ACEF.
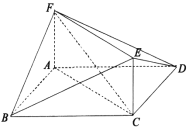
(1)证明:![]() ;
;
(2)求平面BEF与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com