
【题目】如图所示,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]()
![]() 是线段
是线段![]() 的中垂线,
的中垂线,![]()
![]() ,
,![]() 为线段
为线段![]() 上的点.
上的点.

(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
①函数![]() 的最小正周期是
的最小正周期是![]()
②函数![]() 在区间
在区间![]() 上是减函数
上是减函数
③函数![]() 的图像关于点
的图像关于点![]() 对称
对称
④函数![]() 的图像可由函数
的图像可由函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到
个单位得到
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了调查居民的生活水平,随机从小区住户中抽取![]() 个家庭,得到数据如下:
个家庭,得到数据如下:
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式:回归直线的方程是:![]() ,其中,
,其中,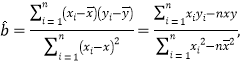
![]() .
.
(1)据题中数据,求月支出![]() (千元)关于月收入
(千元)关于月收入![]() (千元)的线性回归方程(保留一位小数);
(千元)的线性回归方程(保留一位小数);
(2)从这![]() 个家庭中随机抽取
个家庭中随机抽取![]() 个,求月支出都少于
个,求月支出都少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党中央号召,学校以“我们都是追梦人”为主题举行知识竞赛。现有10道题,其中6道甲类题,4道乙类题,王同学从中任取3道题解答.
(Ⅰ)求王同学至少取到2道乙类题的概率;
(Ⅱ)如果王同学答对每道甲类题的概率都是![]() ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是![]() ,且各题答对与否相互独立,已知王同学恰好选中2道甲类题,1道乙类题,用
,且各题答对与否相互独立,已知王同学恰好选中2道甲类题,1道乙类题,用![]() 表示王同学答对题的个数,求随机变量
表示王同学答对题的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产并销售某高科技产品,已知每年生产该产品的固定成本是800万元,生产成本e(单位;万元)与生产的产品件数x(单位:万件)的平方成正比;该产品单价p(单位:元)与生产的产品件数x满足![]() (b为常数),已知当该产品的单价为300元时,生产成本是1800万元,当单价为320元时,生产成本是200万元,且工厂生产的产品都可以销售完.
(b为常数),已知当该产品的单价为300元时,生产成本是1800万元,当单价为320元时,生产成本是200万元,且工厂生产的产品都可以销售完.
(1)每年生产该产品多少万件时,平均成本最低,最低为多少?
(2)若该工厂希望年利润不低于8200万元,则每年大约应该生产多少万件该产品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球的半径为4,球面被互相垂直的两个平面所截,得到的两个圆的公共弦长为2![]() .若球心到这两个平面的距离相等,则这两个圆的半径之和为( )
.若球心到这两个平面的距离相等,则这两个圆的半径之和为( )
A. 4B. 6C. 8D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙三名学生参加某大学的自主招生考试,考试分两轮,第一轮笔试,第二轮面试,只有第一轮笔试通过才有资格进入第二轮面试,面试通过就可以在高考录取中获得该校的优惠加分,两轮考试相互独立.根据以往多次的模拟测试,甲、乙、丙三名学生能通过笔试的概率分别为0.4,0.8,0.5,能通过面试的概率分别为0.8,0.4,0.64.根据这些数据我们可以预测:
(1)甲、乙、丙三名学生中至少有两名学生通过第一轮笔试的概率;
(2)甲、乙、丙三名学生能获得该校优惠加分的人数![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com