Question

已知斜三棱柱ABC-A₁B1C₁的侧面BB₁C₁C与底面ABC垂直，BB₁=BC，∠B₁BC=60°，AB=AC，M是B₁C₁的中点．
（Ⅰ）求证：AB₁∥平面A₁CM；
（Ⅱ）若AB₁与平面BB₁C₁C所成的角为45°，求二面角B-AC-B₁的大小．

Answer 1

分析：（I）先连接AC₁，交A₁C于N，连接MN，根据中位线定理得到MN∥AB₁，再由线面平行的判定定理可证AB₁∥平面A₁CM，得证．
（II）先作BC的中点O，连接AO、B₁O，根据面面垂直的性质定理可知AO⊥面BB₁C₁C，进而知∠AB₁O是AB₁与平面BB₁C₁C所成的角，再由BB₁=BC，∠B₁BC=60°可得△B₁BC是正三角形且B₁O⊥BC，然后以O为原点，分别以OB、OB₁、OA为x轴、y轴、z轴建立直角坐标系，假设OA=a，则可得A、B₁C、O的坐标，进而可表示出

AC

、

AO

、

AB1

的坐标，因为OB₁⊥平面ABC，得到

OB1

是平面ABC的一个法向量，然后表示出平面AB₁C的法向量，可得到＜n₁，n₂＞=arccos

5

5

，即二面角B-AC-B₁的大小是arccos

5

5

．

解答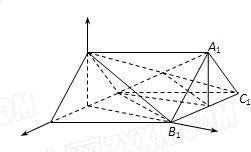：解：（I）证明：如图，连接AC₁，交A₁C于N，连接MN．
∵M是中点，N是AC₁的中点，
∴MN∥AB₁．
∵MN?平面A₁CM，
∴AB₁∥平面A₁CM．
（II）作BC的中点O，连接AO、B₁O．
∵AB=AC，
∴AO⊥BC．
∵侧面BB₁C₁C与底面ABC垂直，
∴AO⊥面BB₁C₁C，
∴∠AB₁O是AB₁与平面BB₁C₁C所成的角，即∠AB₁O=45°，从而AO=B₁O．
又∵BB₁=BC，∠B₁BC=60°，
∴△B₁BC是正三角形，所以B₁O⊥BC．
以O为原点，分别以OB、OB₁、OA为x轴、y轴、z轴建立如图所示空间直角坐标系．
设OA=a，则A（0，0，a），B₁（0，a，0），C（-

3

3

a，0，0），O（0，0，0），
∴

AC

=(-

3

3

a，0，-a)，

AO

=(0，0，-a)，

AB1

=(0，a，-a)．
∵OB₁⊥平面ABC，故

OB1

是平面ABC的一个法向量，设为n₁，
则n₁=

OB1

=(0，a，0)，
设平面AB₁C的法向量为n₂=（x₂，y₂，z₂），
由

AC

•n₂=0且

AB1

•n₂=0得

- 3 3 x2-z2=0 y2-z2=0

令y₂=a，得n₂=（-

3

a，a，a）．
∴cos＜n₁，n₂＞=

n1•n2

|n1|•|n2|

=

1

1× 5

=

5

5

，
∴＜n₁，n₂＞=arccos

5

5

．
即二面角B-AC-B₁的大小是arccos

5

5

．

点评：本题主要考查线面平行的判定定理和用向量的思想解决立体几何中的平面夹角问题．考查考生的知识的综合运用能力和计算能力，用向量的思想解决二面角问题，是这几年高考的热点问题，要强化复习．