
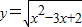 的定义域、值域和单调区间.
的定义域、值域和单调区间. ,结合函数的定义域,由此可得函数的单调区间、减区间.
,结合函数的定义域,由此可得函数的单调区间、减区间.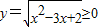 ,故函数的值域为[0,+∞).
,故函数的值域为[0,+∞).  ,且:x∈[2,+∞)∪(-∞,1].
,且:x∈[2,+∞)∪(-∞,1].

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
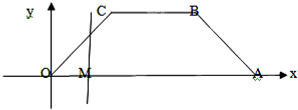 如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.
如图,等腰梯形OABC,底角为45°,各顶点的坐标分别为O(0,0),A(6,0),B(4,2),C(2,2).一条与y轴平行的动直线l从O点开始做平行移动,到A点为止.设直线l与x轴的交点M,记OM=x,记梯形被直线l截得的在l左侧的图形面积为y.| 7 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修1 2.4幂函数练习卷(解析版) 题型:解答题
(本题满分16分)已知幂函数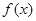 的图象经过点
的图象经过点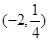 .
.
(Ⅰ) 求函数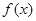 的定义域和值域; (Ⅱ) 证明:函数
的定义域和值域; (Ⅱ) 证明:函数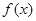 在(0,+
在(0,+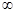 )上是减函数.
)上是减函数.
查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修一3.2对数函数练习卷(二)(解析版) 题型:解答题
已知函数f(x)=loga(a-ax)且a>1,
(1)求函数的定义域和值域;
(2)讨论f(x)在其定义域上的单调性;
(3)证明函数图象关于y=x对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com