练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设等差数列{an}满足3a8=5a15 ， 且 ，Sn为其前n项和，则数列{Sn}的最大项为（ ）
    A.
    B.S24
    C.S25
    D.S26

    【答案】C
    【解析】解：设等差数列{an}的公差为d，∵3a8=5a15，∴3（a1+7d）=5（a1+14d），化为2a1+49d=0，

    ∵ ，∴d＜0，∴等差数列{an}单调递减，

    Sn=na1+ d= + d= （n﹣25）2﹣ d．

    ∴当n=25时，数列{Sn}取得最大值，

    故选：C．

    设等差数列{an}的公差为d，由3a8=5a15，利用通项公式化为2a1+49d=0，由 ，可得d＜0，Sn=na1+ d= （n﹣25）2﹣ d．利用二次函数的单调性即可得出．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线l在x轴上的截距比在y轴上的截距大1，且过点(6，-2)，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】长方体ABCD－A1B1C1D1中，AB＝BC＝2，D1D＝3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系.

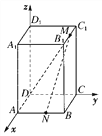
    (1)写出点D、N、M的坐标；

    (2)求线段MD、MN的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）
    A.x，y∈R，若x+y≠0，则x≠1且y≠﹣1
    B.a∈R，“ ＜1“是“a＞1“的必要不充分条件
    C.命题“x∈R，使得x2+2x+3＜0”的否定是“x∈R，都有x2+2x+3＞0”
    D.“若am2＜bm2 ， 则a＜b”的逆命题为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知直角梯形ACDE所在的平面垂直于平面ABC，∠BAC=

    ∠ACD=90°，∠EAC=60°，AB=AC=AE.

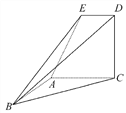
    (1)在直线BC上是否存在一点P，使得DP∥平面EAB？请证明你的结论.

    (2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在Rt△AOB中，AO=1，BO=2，如图，动点P是在以O点为圆心，OB为半径的扇形内运动（含边界）且∠BOC=90°；设 ，则x+y的取值范围 ．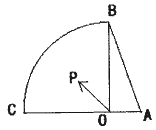

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥P－ABCD的底面ABCD是正方形，E，F分别为AC和PB上的点，它的直观图，正视图，侧视图如图所示.

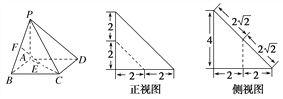
    (1)求EF与平面ABCD所成角的大小；

    (2)求二面角B－PA－C的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在Rt△ABC中，∠C=90°，BC=6，AC=3，D，E分别是AC，AB上的点，且DE∥BC，DE=4，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．

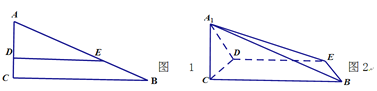
    （1）求证：平面；

    （2）过点E作截面 平面，分别交CB于F，于H，求截面的面积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在底面为平行四边形的四棱锥P﹣ABCD中，PA⊥平面ABCD，且BC=2AB═4，∠ABC=60°，点E是PD的中点．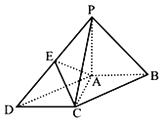
    （1）求证：AC⊥PB；
    （2）当二面角E﹣AC﹣D的大小为45°时，求AP的长．

    查看答案和解析>>

    同步练习册答案