
【题目】给定函数![]() ,若对于定义域中的任意
,若对于定义域中的任意![]() ,都有
,都有![]()
![]() 恒成立,则称函数
恒成立,则称函数![]() 为“爬坡函数”.
为“爬坡函数”.
(Ⅰ)证明:函数![]() 是“爬坡函数”;
是“爬坡函数”;
(Ⅱ)若函数![]() 是“爬坡函数”,求实数
是“爬坡函数”,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若对任意的实数![]() ,函数
,函数![]() 都不是“爬坡函数”,求实数
都不是“爬坡函数”,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t![]() 1,不等式f(
1,不等式f(![]() )+f(
)+f(![]() )<0恒成立,求k的取值范围.
)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,且f(α)=1,α∈(0, ![]() ),则cos(2
),则cos(2 ![]() )=( )
)=( )
A.![]()
B.![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣lnx.
(参考数据:e≈2.718,ln2≈0.693,ln3≈1.099,ln5≈1.609,ln7≈1.946)
(1)求证:函数f(x)有且只有一个极值点x0;
(2)求函数f(x)的极值点x0的近似值x′,使得|x′﹣x0|<0.1;
(3)求证:f(x)>2.3对x∈(0,+∞)恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“招手即停”公共汽车的票价按下列规则制定:
5公里以内(含5公里),票价2元;
5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,请根据题意.
(1)写出票价与里程之间的函数解析式;
(2)根据(1)写出的函数解析式试画出该函数的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(1)=1,且对任意的x∈R,都有f′(x)< ![]() ,则不等式f(log2x)>
,则不等式f(log2x)> ![]() 的解集为( )
的解集为( )
A.(1,+∞)
B.(0,1)
C.(0,2)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱猪ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E为棱AA1的中点.
(1)证明:B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图给出的是计算 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() 的值的程序框图,其中判断框内应填入的是( )
的值的程序框图,其中判断框内应填入的是( ) 
A.i≤4030?
B.i≥4030?
C.i≤4032?
D.i≥4032?
查看答案和解析>>
科目:高中数学 来源: 题型:
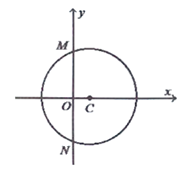
【题目】已知圆心在x轴正半轴上的圆C与直线![]() 相切,与y轴交于M,N两点,且
相切,与y轴交于M,N两点,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求圆C的标准方程;
求圆C的标准方程;
![]() Ⅱ
Ⅱ![]() 过点
过点![]() 的直线l与圆C交于不同的两点D,E,若
的直线l与圆C交于不同的两点D,E,若![]() 时,求直线l的方程;
时,求直线l的方程;
![]() Ⅲ
Ⅲ![]() 已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得
已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得![]() ?若存在,求出A,B两点的坐标;若不存在,请说明理由.
?若存在,求出A,B两点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com