
![]()
图1 图2
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:022
(2004
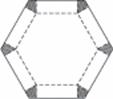
福建,16)如图所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为___________时,其容积最大.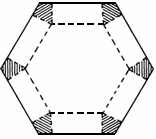
查看答案和解析>>
科目:高中数学 来源:2011届江苏省南京六中高三下学期期中考试理数 题型:解答题
(本题满分16分)
如图,直角三角形ABC中,∠B= ,AB=1,B
,AB=1,B C=
C= .点M,N分别在边AB和AC
.点M,N分别在边AB和AC
上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△ MN,使顶点
MN,使顶点 落
落
在边BC上( 点和B点不重合).设∠AMN=
点和B点不重合).设∠AMN= .
.
(1) 用 表示线段
表示线段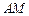 的长度,并写出
的长度,并写出 的取值范围;
的取值范围;
(2) 求线段 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
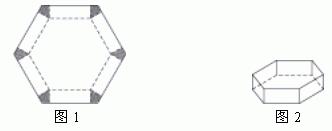
如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,当这个正六棱柱容器的底面边长为 时,其容积最大.
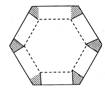 (第16题图)
(第16题图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com