
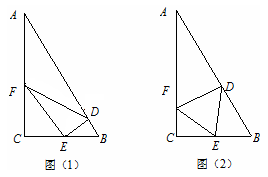
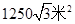 ;(2)
;(2)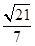 百米.
百米.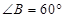 ,由于EF‖AB,EF⊥ED,那么有
,由于EF‖AB,EF⊥ED,那么有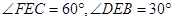 ,因此我们可用CE来表示FE,DE.从而把S△DEF表示为CE的函数,然后利用函数的知识(或不等式知识)求出最大值;(2).等边△DEF可由两边EF=ED及
,因此我们可用CE来表示FE,DE.从而把S△DEF表示为CE的函数,然后利用函数的知识(或不等式知识)求出最大值;(2).等边△DEF可由两边EF=ED及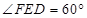 确定,我们设
确定,我们设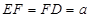 ,想办法也把
,想办法也把 与一个参数建立关系式,关键是选取什么为参数,由于等边△DEF位置不确定,我们可选取
与一个参数建立关系式,关键是选取什么为参数,由于等边△DEF位置不确定,我们可选取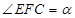 为参数,建立起
为参数,建立起 与
与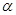 的关系.
的关系.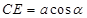 ,则
,则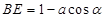 ,
,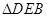 中应用正弦定理可建立所需要的等量关系.
中应用正弦定理可建立所需要的等量关系.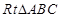 中,
中,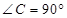 ,
,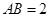 百米,
百米,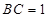 百米.
百米.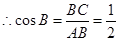 ,可得
,可得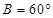 ,
,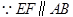 ,
,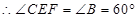 ,
,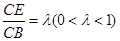 ,则
,则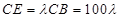 米,
米,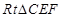 中,
中,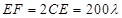 米,C到EF的距离
米,C到EF的距离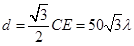 米,
米,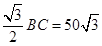 米,
米,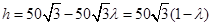 米,
米,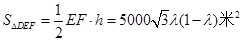 ,
,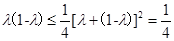 ,当且仅当
,当且仅当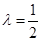 时等号成立,
时等号成立,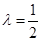 时,即E为AB中点时,
时,即E为AB中点时,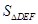 的最大值为
的最大值为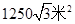 .7分
.7分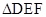 的边长为
的边长为 ,
,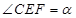 ,
,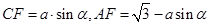 ,
,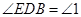 ,可得
,可得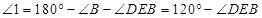 ,
,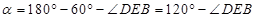 ,
,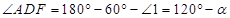 .
.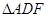 中,
中,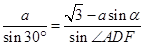 ,
,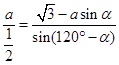 ,化简得
,化简得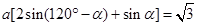 ,12分
,12分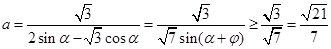 (其中
(其中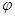 是满足
是满足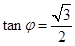 的锐角),
的锐角),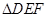 边长最小值为
边长最小值为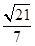 百米.14分
百米.14分

科目:高中数学 来源:不详 题型:解答题
 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按 米处理).
米处理).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com