
【题目】设椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由.
【答案】
(1)解:∵原点、焦点,短轴的端点构成等腰直角三角形,∴b=c,
∵椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),∴
),∴ ![]() =1,
=1,
联立 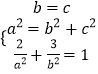 ,解得b=c=2,a2=8.
,解得b=c=2,a2=8.
∴椭圆E的方程为 ![]() =1
=1
(2)解:假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() .
.
设圆的方程为:x2+y2=r2,(0<r<2).
设圆的切线为y=kx+m,则 ![]() =r,A(x1,y1),B(x2,y2).
=r,A(x1,y1),B(x2,y2).
联立 ![]() ,化为:(1+2k2)x2+4kmx+2m2﹣8=0,
,化为:(1+2k2)x2+4kmx+2m2﹣8=0,
△≥0,可得:9k2+4≥m2.
x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
∵ ![]() ,∴
,∴ ![]() =x1x2+y1y2=0.
=x1x2+y1y2=0.
∴(1+k2)x1x2+mk(x1+x2)+m2=0,
∴ ![]() ﹣
﹣ ![]() +m2=0,
+m2=0,
化为:3m2=8+8k2,与 ![]() =r联立,
=r联立,
可得r2= ![]() =
= ![]() =
= ![]() <4,
<4,
因此假设成立,存在圆心在原点的圆,方程为x2+y2= ![]() ,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B,且
,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B,且 ![]()
【解析】(1)由原点、焦点,短轴的端点构成等腰直角三角形,可得b=c.由椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),可得
),可得 ![]() =1,与a2=b2+c2联立即可得出.(2)假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且
=1,与a2=b2+c2联立即可得出.(2)假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() .设圆的方程为:x2+y2=r2 , (0<r<2).设圆的切线为y=kx+m,可得
.设圆的方程为:x2+y2=r2 , (0<r<2).设圆的切线为y=kx+m,可得 ![]() =r,A(x1 , y1),B(x2 , y2).与椭圆方程联立化为:(1+2k2)x2+4kmx+2m2﹣8=0,利用根与系数的关系及其
=r,A(x1 , y1),B(x2 , y2).与椭圆方程联立化为:(1+2k2)x2+4kmx+2m2﹣8=0,利用根与系数的关系及其 ![]() ,可得
,可得 ![]() =x1x2+y1y2=0.化简整理即可得出.
=x1x2+y1y2=0.化简整理即可得出.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左焦点
的左焦点![]() 左顶点
左顶点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知![]() ,
,![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.若
两侧的动点.若![]() ,试问直线
,试问直线![]() 的斜率是否为定值?请说明理由.
的斜率是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将该产品的年利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家年促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心![]() 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切且被轴
相切且被轴![]() 截得的弦长为
截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C1的方程为ρsin(θ+ ![]() )+2
)+2 ![]() =0,曲线C2的参数方程为
=0,曲线C2的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)将C1的方程化为直角坐标方程;
(2)若点Q为C2上的动点,P为C1上的动点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象经过
的图象经过![]() 和
和![]() 两点,如图所示,且函数
两点,如图所示,且函数![]() 的值域为
的值域为![]() .过该函数图象上的动点
.过该函数图象上的动点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
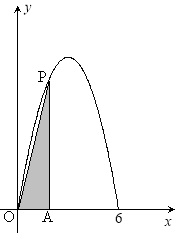
(I)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com