
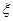 ,求
,求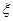 的分布列及数学期望E
的分布列及数学期望E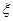 .
.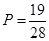 ;(Ⅱ)分布列为:
;(Ⅱ)分布列为: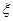 | 1 | 2 | 3 |
 | 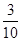 | 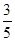 | 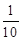 |
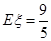 .
. ,再求出符合条件的基本事件数,摸出的2个小球为异色球的种数为
,再求出符合条件的基本事件数,摸出的2个小球为异色球的种数为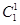
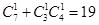 ,从而求出概率
,从而求出概率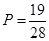 ;(Ⅱ)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,此时有三种:一种是有1个红球,1个黑球,1个白球,二种是有2个红球,1个其它颜色球,三种是所摸得的3小球均为红球,分别求出它们的概率,得分布列,从而求出期望.
;(Ⅱ)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,此时有三种:一种是有1个红球,1个黑球,1个白球,二种是有2个红球,1个其它颜色球,三种是所摸得的3小球均为红球,分别求出它们的概率,得分布列,从而求出期望.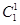
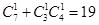 2分
2分 3分
3分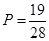 6分
6分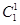
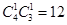 种 7分
种 7分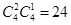 种, 8分
种, 8分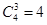 种不同摸法,
种不同摸法,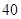 种. 10分
种. 10分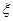 的取值为
的取值为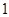 ,
,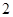 ,
,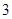 .其分布列为:
.其分布列为: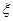 | 1 | 2 | 3 |
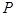 | 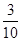 | 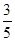 | 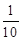 |
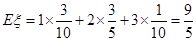 12分
12分

 口算能手系列答案
口算能手系列答案科目:高中数学 来源:不详 题型:解答题
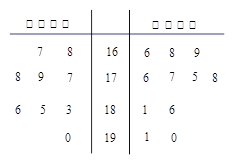
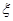 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出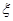 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
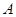 和获得等级不是
和获得等级不是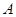 的机会相等,物理、化学、生物获得等级
的机会相等,物理、化学、生物获得等级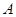 的事件分别记为
的事件分别记为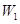 、
、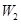 、
、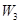 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是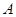 的事件分别记为
的事件分别记为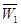 、
、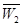 、
、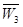 .
.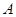 的所有可能结果(如三科成绩均为
的所有可能结果(如三科成绩均为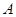 记为
记为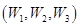 );
);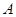 的概率;
的概率;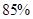 ,并说明理由.
,并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.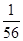 ; ; | B.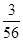 ; ; | C.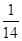 ; ; | D.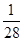 . . |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com