
已知函数f(x)= ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
见解析
【解析】
试题分析:本题是一个比较复杂的函数求零点的问题,通过转化为两个较熟悉的函数研究.容易得到两个数有三个交点,所以有三个零点.零点的范围不好确定,本题很巧妙地应用了零点定理,求出了个的范围.这种方法值得好好体会.
试题解析:由f(x)=0,得 ,令
,令 ,
, .分别画出它们的图象如图,其中抛物线的顶点坐标为(0,2),与x轴的交点为(-2,0)、(2,0),
.分别画出它们的图象如图,其中抛物线的顶点坐标为(0,2),与x轴的交点为(-2,0)、(2,0), 与
与 的图象有3个交点,从而函数f(x)有3个零点.由f(x)的解析式知x≠0,f(x)的图象在(-∞,0)和(0,+∞)上分别是连续不断地曲线,且
的图象有3个交点,从而函数f(x)有3个零点.由f(x)的解析式知x≠0,f(x)的图象在(-∞,0)和(0,+∞)上分别是连续不断地曲线,且
 即
即 ,
, .所以三个零点分别在区间(-3,-2),
.所以三个零点分别在区间(-3,-2), ,(1,2)内.
,(1,2)内.

考点:1.函数的零点转化为图解.2.零点定理.3.列举发现问题的思维.


科目:高中数学 来源:2016届广东广州执信中学高一上学期期末考试数学试卷(解析版) 题型:选择题
已知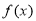 是定义在
是定义在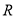 上的偶函数,它在
上的偶函数,它在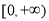 上是减函数,若
上是减函数,若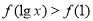 ,则
,则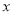 的取值范围是( )
的取值范围是( )
A.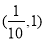 B.
B.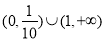
C.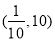 D.
D.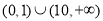
查看答案和解析>>
科目:高中数学 来源:2016届广东实验中学高一一级模块考试数学试卷(解析版) 题型:选择题
右图是水平放置的 的直观图,
的直观图, 轴,
轴, ,则
,则 是( )
是( )

A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源:2016届山西省高一年级月考(三)数学试卷(解析版) 题型:选择题
下图给出的是计算 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )

A.i>100 B.i<=100 C.i>50 D.i<=50
查看答案和解析>>
科目:高中数学 来源:2016届山东省滕州市高一(上)期末考试数学试家(解析版) 题型:选择题
已知平面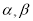 ,直线
,直线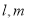 ,且有
,且有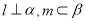 ,则下列四个命题正确的个数为( )
,则下列四个命题正确的个数为( )
①若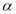 ∥
∥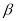 则
则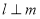 ;②若
;②若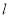 ∥
∥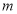 则
则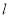 ∥
∥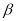 ;③若
;③若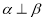 则
则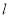 ∥
∥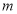 ;④若
;④若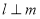 则
则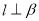 ;
;
A.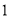 B.
B.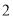 C.
C.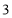 D.
D.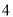
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com