

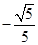
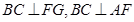 ,而折叠后直线
,而折叠后直线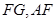 变为两条相交直线,因此可由线面垂直判定定理得到BC⊥平面AFG ,(2)求二面角,有两个方法,一是作出二面角的平面角,二是利用空间向量计算;本题易建立空间直角坐标系,较易表示各点坐标,因此选择利用空间向量求二面角.下面的关键是求出两个平面的法向量,平面ADE的一个法向量易求,而平面ABE的一个法向量则需列方程组求解,最后利用数量积求夹角的余弦值
变为两条相交直线,因此可由线面垂直判定定理得到BC⊥平面AFG ,(2)求二面角,有两个方法,一是作出二面角的平面角,二是利用空间向量计算;本题易建立空间直角坐标系,较易表示各点坐标,因此选择利用空间向量求二面角.下面的关键是求出两个平面的法向量,平面ADE的一个法向量易求,而平面ABE的一个法向量则需列方程组求解,最后利用数量积求夹角的余弦值
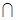 FG=F,所以DE⊥平面AFG.
FG=F,所以DE⊥平面AFG.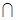 平面BCDE=DE,DE⊥AF,DE⊥GF,所以FA,FD,FG两两垂直.
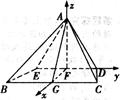
平面BCDE=DE,DE⊥AF,DE⊥GF,所以FA,FD,FG两两垂直.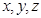 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系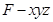 .
.
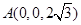 ,
,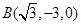 ,
,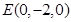 ,所以
,所以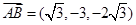 ,
,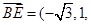 0). 6分
0). 6分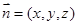 .
.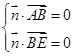 ,即
,即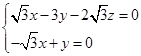 ,
,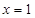 ,则
,则 ,
,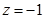 ,则
,则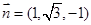 . 8分
. 8分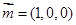 为平面ADE的一个法向量,
为平面ADE的一个法向量, . 10分
. 10分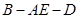 为钝角,所以二面角
为钝角,所以二面角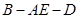 的余弦值为
的余弦值为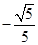 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
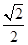 AB.
AB.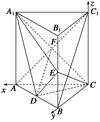
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.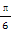 | B. | C.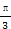 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.n1=(1,2,1),n2=(-3,1,1) |
| B.n1=(1,1,2),n2=(-2,1,1) |
| C.n1=(1,1,1),n2=(-1,2,1) |
| D.n1=(1,2,1),n2=(0,-2,-2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
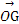 =x
=x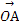 +y
+y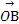 +z
+z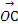 ,则(x,y,z)为( )
,则(x,y,z)为( )A.( , , , , ) ) | B.( , , , , ) ) |
C.( , , , , ) ) | D.( , , , , ) ) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
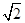 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.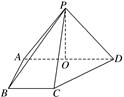
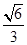 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(-1, -2, 3) | B.(1, 2, -3) | C.(-1, -2, -3) | D.(-1, 2, -3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com