
【题目】下列说法错误的是( )
A. “sinθ=![]() ”是“θ=30°”的充分不必要条件
”是“θ=30°”的充分不必要条件
B. 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”
C. △ABC中,“sin A>sin B”是“A>B”的充要条件
D. 如果命题“綈p”与命题“p∨q”都是真命题,那么命题q一定是真命题
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为( )
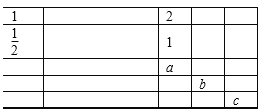
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的个数为:( )
①![]() 的图像关于点
的图像关于点![]() 对称;②
对称;②![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③![]() 的图像关于直线
的图像关于直线![]() 对称;④
对称;④![]() 的图像关于直线
的图像关于直线![]() 对称。
对称。
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当∠AOB为锐角时,求k的取值范围;
,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点。
是否过定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
①若tan θ=2,则sin 2θ=![]() ;
;
②函数f(x)=lg(x+![]() )是奇函数;
)是奇函数;
③“a>b”是“2a>2b”的充分不必要条件;
④在△ABC中,若sin Acos B=sin C,则△ABC是直角三角形.
其中所有真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(1+x)+lg(1﹣x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是100(5x+1﹣ ![]() )元.
)元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com