
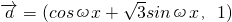 ,
, ,其中ω>0且
,其中ω>0且 ,函数f(x)的图象两相邻对称轴之间的距离为
,函数f(x)的图象两相邻对称轴之间的距离为 .
.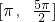 上的最大值及相应的x的值.
上的最大值及相应的x的值. 得
得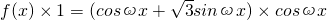 ,整理并化简得
,整理并化简得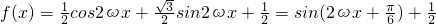 ,
,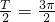 ,T=3π,又
,T=3π,又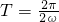 ,
, .
.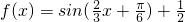 ,
,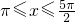 ,
,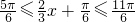 ,
,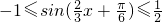 ,
,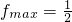 ,易得相应的x=π.
,易得相应的x=π.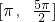 ,求出
,求出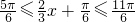 ,
,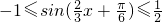 即求函数f(x)在区间的最大值及相应的x的值.
即求函数f(x)在区间的最大值及相应的x的值.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省实验中学、华南师大附中、广西梧州中学等四校高三联考数学试卷(理科)(解析版) 题型:解答题
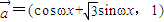 ,
,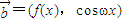 ,其中ω>0且
,其中ω>0且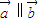 ,函数f(x)的图象两相邻对称轴之间的距离为
,函数f(x)的图象两相邻对称轴之间的距离为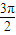 .
.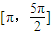 上的最大值及相应的x的值.
上的最大值及相应的x的值.查看答案和解析>>
科目:高中数学 来源:2010年广东省江门市高考数学后阶段备考指导和猜题试卷(解析版) 题型:解答题
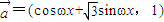 ,
,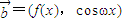 ,其中ω>0且
,其中ω>0且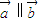 ,函数f(x)的图象两相邻对称轴之间的距离为
,函数f(x)的图象两相邻对称轴之间的距离为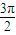 .
. 上的最大值及相应的x的值.
上的最大值及相应的x的值.查看答案和解析>>
科目:高中数学 来源:2011年高考数学综合复习试卷(2)(解析版) 题型:解答题
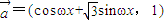 ,
, ,其中ω>0且
,其中ω>0且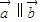 ,函数f(x)的图象两相邻对称轴之间的距离为
,函数f(x)的图象两相邻对称轴之间的距离为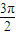 .
. 上的最大值及相应的x的值.
上的最大值及相应的x的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com