
【题目】已知抛物线L:![]() (
(![]() )的焦点为F,过点
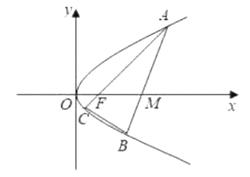
)的焦点为F,过点![]() 的动直线l与抛物线L交于A,B两点,直线
的动直线l与抛物线L交于A,B两点,直线![]() 交抛物线L于另一点C,直线
交抛物线L于另一点C,直线![]() 的最小值为4.
的最小值为4.
(1)求椭圆C的方程;
(2)若过点A作y轴的垂线m,则x轴上是否存在一点![]() ,使得直线PB与直线m的交点恒在一条定直线上?若存在,求该点的坐标及该定直线的方程;若不存在,请说明理由.
,使得直线PB与直线m的交点恒在一条定直线上?若存在,求该点的坐标及该定直线的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ,
,![]() .
.
【解析】
(1)显然当![]() 轴时,
轴时,![]() 取得最小值,可得
取得最小值,可得![]() ,即可得到所求抛物线方程;
,即可得到所求抛物线方程;
(2)假设![]() 轴上存在一点
轴上存在一点![]() ,
,![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 的交点恒在一条定直线上.设
的交点恒在一条定直线上.设![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立抛物线方程,运用韦达定理,由
,联立抛物线方程,运用韦达定理,由![]() 的方程和直线
的方程和直线![]() 的方程,联立求得交点,化简可得所求定点和定直线.
的方程,联立求得交点,化简可得所求定点和定直线.
(1)设直线![]() 的倾斜角为
的倾斜角为![]() ,
,
所以由抛物线![]() (
(![]() )的焦点弦公式得
)的焦点弦公式得![]() ,
,
所以当![]() ,即当
,即当![]() 轴时,
轴时,![]() 取得最小值.
取得最小值.
把![]() 代入
代入![]() 可得
可得![]() ,
,
故![]() ,
,![]() ,
,
可得抛物线的方程为:![]() .
.
(2)假设![]() 轴上存在一点
轴上存在一点![]() ,
,![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 的交点恒在一条定直线上.
的交点恒在一条定直线上.
设![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立抛物线方程![]() ,可得
,可得![]() ,
,
![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() 即
即![]() ,
,
联立直线![]() ,
,
可得![]() ,
,
由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
即有![]() ,
,
由假设可得![]() ,
,
即![]() ,此时
,此时![]() ,
,
可得存在定点![]() ,定直线为
,定直线为![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有两个不等实根的概率.
三个数中任取的一个数,求上述方程有两个不等实根的概率.
(2)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西安市自2017年5月启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,斑马线前礼让行人也成为了一张新的西安“名片”.
但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患及机动车通畅率降低,交警部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到![]() 列联表如下:
列联表如下:
30岁以下 | 30岁以上 | 合计 | |
闯红灯 | 60 | ||
未闯红灯 | 80 | ||
合计 | 200 |
近期,为了整顿“行人闯红灯”这一不文明及项违法行为,交警部门在该十字路口试行了对闯红灯行人进行经济处罚,并从试行经济处罚后穿越该路口行人中随机抽取了200人进行调查,得到下表:
处罚金额 | 5 | 10 | 15 | 20 |
闯红灯的人数 | 50 | 40 | 20 | 0 |
将统计数据所得频率代替概率,完成下列问题.
(Ⅰ)将![]() 列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
列联表填写完整(不需写出填写过程),并根据表中数据分析,在未试行对闯红灯行人进行经济处罚前,是否有99.9%的把握认为闯红灯与年龄有关;
(Ⅱ)当处罚金额为10元时,行人闯红灯的概率会比不进行处罚降低多少;
(Ⅲ)结合调查结果,谈谈如何治理行人闯红灯现象.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.132 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年冬奥会,某市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如图所示的茎叶图:
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如图所示的茎叶图:

(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核为优秀的概率;
(2)从图中考核成绩满足![]() 的学生中任取3人,设
的学生中任取3人,设![]() 表示这3人中成绩满足
表示这3人中成绩满足![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据以往培训数据,规定当![]() 时培训有效.请你根据图中数据,判断此次冰雪培训活动是否有效,并说明理由.
时培训有效.请你根据图中数据,判断此次冰雪培训活动是否有效,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,椭圆C截直线y=1所得线段的长度为
,椭圆C截直线y=1所得线段的长度为![]() .
.
(Ⅰ)求椭圆C的方程;
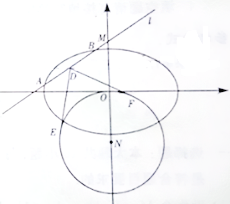
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求![]() EDF的最小值.
EDF的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
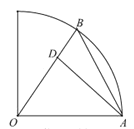
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com