
【题目】定义函数F(a,b)= ![]() (a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
(a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
A.4
B.6
C.![]()
D.![]()
【答案】B
【解析】解:∵F(a,b)= ![]() (a+b﹣|a﹣b|)=
(a+b﹣|a﹣b|)= ![]() ,
,
∴设G(x)=F(f(x),g(x))= ![]() .
.
∵当﹣1≤x≤2时,f(x)≥g(x),此时G(x)=x+2∈[1,4],
此时函数无零点,此时最大值为4,
当x>2或x<﹣1时,f(x)<g(x),G(x)=﹣x2+2x+4=﹣(x﹣1)2+3<4,
综上可得,函数G(x)的最大值为4,
由G(x)=﹣x2+2x+4=0,得方程的两根之和为2,
则函数F(f(x),g(x))的最大值与零点之和为2+4=6,
故选:B.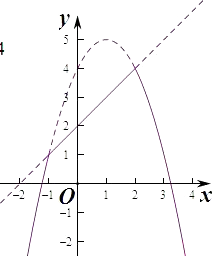
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在坐标原点,左、右焦点F1、F2分别在x轴上,离心率为 ![]() ,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
,在其上有一动点A,A到点F1距离的最小值是1,过A、F1作一个平行四边形,顶点A、B、C、D都在椭圆E上,如图所示.
(Ⅰ)求椭圆E的方程;
(Ⅱ)判断ABCD能否为菱形,并说明理由.
(Ⅲ)当ABCD的面积取到最大值时,判断ABCD的形状,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形,高AA1= ![]() ,点A是平面α内的一个定点,AA1与α所成角为
,点A是平面α内的一个定点,AA1与α所成角为 ![]() ,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= .
,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解某地区电视观众对某类体育节目的收视情况随机抽取了100名观众进行调查,其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
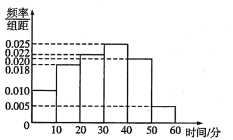
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别有关?
列联表,并据此资料你是否认为“体育迷”与性别有关?
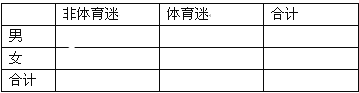
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求证: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求证: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域
的定义域![]() ,值域是
,值域是![]() ;
;![]() 定义域
定义域![]() ,值域是
,值域是![]() ,其中实数
,其中实数![]() 满足
满足![]() .
.
甲:如果任意![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
乙:如果存在![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丙:如果任意![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丁:如果存在![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
请判断上述四个命题中,假命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知存在常数![]() ,那么函数
,那么函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,再由函数的奇偶性可知在
上是增函数,再由函数的奇偶性可知在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(1)判断函数![]() 的单调性,并证明:
的单调性,并证明:
(2)将前述的函数![]() 和
和![]() 推广为更为一般形式的函数
推广为更为一般形式的函数![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的单调性(只须归纳出结论,不必推理证明)
的单调性(只须归纳出结论,不必推理证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过两个焦点,A,B是椭圆C的长轴端点.
=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过两个焦点,A,B是椭圆C的长轴端点. 
(1)求椭圆C的标准方程和圆O的方程;
(2)设P、Q分别是椭圆C和圆O上位于y轴两侧的动点,若直线PQ与x平行,直线AP、BP与y轴的交点即为M、N,试证明∠MQN为直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 给定两个命题![]() ,若
,若![]() 为真命题,则
为真命题,则![]() 都是假命题;
都是假命题;
B. 命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”;
”;
C. 若命题![]() ,则
,则![]() ,使得
,使得![]() ;
;
D. 函数![]() 在
在![]() 处的导数存在,若
处的导数存在,若![]() 是
是![]() 的极值点,则
的极值点,则![]() 是
是![]() 的充要条件.
的充要条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com