
���� ��1�����ݶ������ź����Ķ��壬ֱ�Ӵ��������ֵ���ɣ�
��2�����ݺ������Ķ���������жϺ���y=f��x��-x�ڣ�1��+�ޣ�������㣻
��3������k�����ź�����������������������ϵ����������ۣ�
��� �⣺��1����$\sqrt{2}$�ʣ�1��2]�ã�f��$\sqrt{2}$��=1+1+log${\;}_{\frac{1}{2}}$$\sqrt{2}$=$\frac{1}{2}$����2�֣�
������������f��2$\sqrt{2}$��=2f��$\sqrt{2}$��=2��$\frac{1}{2}$=1����4�֣�
��2����x�ʣ�2i��2i+1]��i=0��1��2��ʱ��$\frac{x}{{2}^{i}}$�ʣ�1��2]��������ɵã�f��x��=2f��$\frac{x}{2}$��=22f��$\frac{x}{{2}^{2}}$��=��=2if��$\frac{x}{{2}^{i}}$��=2i$\sqrt{2•\frac{x}{{2}^{i}}-��\frac{x}{{2}^{i}}��^{2}}$=$\sqrt{{2}^{i+1}x-{x}^{2}}$������6�֣�
����f��x��-x=0?$\sqrt{{2}^{i+1}x-{x}^{2}}$=x?x=0��x=2i��0��2i�������ڣ�2i��2i+1]����i=0��1��2��������8�֣�
��x�ʣ�2i��2i+1]����i=0��1��2����ʱ������f��x��-x=0��ʵ���⣮
ע���1��+�ޣ�=��20��21]�ȣ�21��22]�ȣ�22��23���ȡ������Ժ���y=f��x��-x�ڣ�1��+�ޣ�������㣮����10�֣�
��3����x�ʣ�kj��kj+1]��j��Zʱ����$\frac{x}{{k}^{j}}$�ʣ�1��k]��������ɵã�f��x��=kf��$\frac{x}{k}$��=k2f��$\frac{x}{{k}^{2}}$��=��=kjf��$\frac{x}{{k}^{j}}$��
��x�ʣ�1��k]ʱ��f��x����ȡֵ��Χ��[0��1������12�֣�
���Ե�x�ʣ�kj��kj+1]��j��Zʱ��f��x����ȡֵ��Χ��[0��kj��������14�֣�
���ڣ�0��kn+1]=��kn��kn+1]�ȣ�kn-1��kn]�ȡ��ȣ�k0��k]�ȣ�k-1��k0]�ȡ���16�֣�
���Ժ���f��x���ڣ�0��kn+1]��n��N���ϵ�ȡֵ��Χ�ǣ�[0��kn����[0��kn-1���ȡ���[0��k0����[0��k-1���ȡ�=[0��kn��������18�֣�
���� ������Ҫ�����¶����Ӧ�ã���ȷ����k�����ź����Ķ����ǽ������Ĺؼ����ۺ���ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���⡰��x2=1����x=1���ķ�����Ϊ������x2=1��x��1�� | |
| B�� | ��x=-1���ǡ�x2-5x-6=0���ı�Ҫ��������� | |
| C�� | ���⡰?x��R��ʹ��x2+x+1��0���ķ��ǣ���?x��R������x2+x+1��0�� | |
| D�� | ���⡰��sinx��siny����x��y��Ϊ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�ADΪ�ڽ�ƽ���ߣ���ADC=60�㣬��E��AD�ϣ�����DE=DB������CE��AB�ڵ�F����֤��AF•AB+CD•CB=AC2��
��ͼ���ڡ�ABC�У�ADΪ�ڽ�ƽ���ߣ���ADC=60�㣬��E��AD�ϣ�����DE=DB������CE��AB�ڵ�F����֤��AF•AB+CD•CB=AC2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 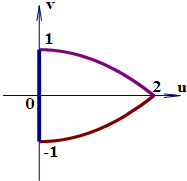 | B�� | 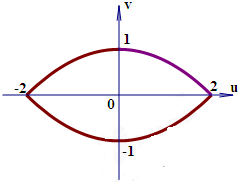 | ||
| C�� | 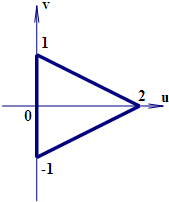 | D�� | 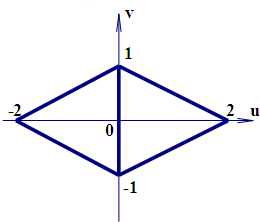 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com