
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
分析 (1)设乙公司快递员送快递单数为a,由a的不同取值求出相应在的X,得到X的所有可能取值为152,156,160,166,172,由此能求出X的分布列和E(X).
(2)依题意,能求出甲公司快递员日平均快递单数,从而能求出甲公司送餐员日平均工资,再求出乙公司送餐员日平均工资,由此推荐小明去乙公司应聃.
解答 解:(1)设乙公司快递员送快递单数为a,
当a=38时,X=38×4=152,
当a=39时,X=39×4=156,
当a=40时,X=40×4=160,
当a=41时,X=40×4+1×6=166,
当a=42时,X=40×4+2×6=172,
∴X的所有可能取值为152,156,160,166,172,
∴X的分布列为:
| X | 152 | 156 | 160 | 166 | 172 |
| P | $\frac{1}{10}$ | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{2}{5}$ | $\frac{1}{10}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | K 2>3.841 | B. | K 2<3.841 | C. | K 2>6.635 | D. | K 2<6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的一条对称轴为x=$\frac{5π}{12}$ | |
| B. | 存在φ使得f(x)在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | |
| C. | f(x)的一个对称中心为($\frac{5π}{12}$,0) | |
| D. | 存在φ使得f(x)在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
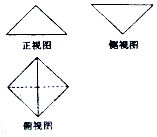 如图是一个几何体的三视图,其中正视图和侧视图是高为2,底边长为$2\sqrt{2}$的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是4$\sqrt{3}$π.
如图是一个几何体的三视图,其中正视图和侧视图是高为2,底边长为$2\sqrt{2}$的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是4$\sqrt{3}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com