
【题目】已知函数![]() 是定义在R上的奇函数,其中
是定义在R上的奇函数,其中![]() 为指数函数,且
为指数函数,且![]() 的图象过定点
的图象过定点![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于x的方程,![]() 有解,求实数a的取值范围;
有解,求实数a的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)设出![]() 的解析式,根据点
的解析式,根据点![]() 求得
求得![]() 的解析式.根据
的解析式.根据![]() 为奇函数,求得
为奇函数,求得![]() 解析式.
解析式.
(2)根据![]() 的单调性和值域,求得
的单调性和值域,求得![]() 的取值范围.
的取值范围.
(3)证得![]() 的单调性,结合
的单调性,结合![]() 的奇偶性化简不等式
的奇偶性化简不等式![]() ,得到对任意的
,得到对任意的![]() ,
,![]() ,利用二次函数的性质求得
,利用二次函数的性质求得![]() 的取值范围.
的取值范围.
(1)设![]() (
(![]() ,且
,且![]() ),则
),则![]() ,
,
所以![]() (舍去)或
(舍去)或![]() ,
,
所以![]() ,
,![]() .
.
又![]() 为奇函数,且定义域为R,
为奇函数,且定义域为R,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() .
.
(2)由于![]() 为
为![]() 上减函数,由于
上减函数,由于![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(3)设![]() ,
,
则![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以函数![]() 在R上单调递减.
在R上单调递减.
要使对任意的![]() ,
,
![]() 恒成立,
恒成立,
即对任意的![]() ,
,
![]() 恒成立.
恒成立.
因为![]() 为奇函数,
为奇函数,
所以![]() 恒成立.
恒成立.
又因为函数![]() 在R上单调递减,
在R上单调递减,
所以对任意的![]() ,
,![]() 恒成立,
恒成立,
即对任意的![]() ,
,![]() 恒成立.
恒成立.
令![]() ,
,![]() ,
,
![]() 时,
时,![]() 成立;
成立;
![]() 时,
时,![]()
所以,![]() .
.
![]() ,
,![]() ,无解.
,无解.
综上,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产![]() (千部)手机,需另投入成本
(千部)手机,需另投入成本![]() 万元,且
万元,且  ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(![]() )求出2020年的利润
)求出2020年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
![]() 2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响某校随机抽取200名学生,对学习成绩和学案使用程度进行了调查,统计数据如下表所示:
善于使用学案 | 不善于使用学案 | 合计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
合计 | 200 |
已知随机抽查这200名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
参考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(I)完成![]() 列联表(不用写计算过程);
列联表(不用写计算过程);
(Ⅱ)试运用独立性检验的思想方法分析有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体素质情况,现从我校学生中随机抽取10人进行体能测试,测试的分数(百分制)如茎叶图所示.根据有关国家标准,成绩不低于79分的为优秀,将频率视为概率.
(1)另从我校学生中任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(2)从前文所指的这10人(成绩见茎叶图)中随机选取3人,记![]() 表示测试成绩为“优秀”的学生人数,求
表示测试成绩为“优秀”的学生人数,求![]() 的分布列及期望.
的分布列及期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前共享单车基本覆盖饶城市区,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
(1)任选出一名学生,求他(她)骑行过共享单车的概率;
(2)随着单车投放数量增加,乱停乱放成为城市管理的问题,如表是本市某组织累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间关系图表:
之间关系图表:
累计投放单车数量 | 100000 | 120000 | 150000 | 200000 | 230000 |
乱停乱放单车数量 | 1400 | 1700 | 2300 | 3000 | 3600 |
计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() ,
,![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
(3)已知信州区、广丰区、上饶县、经开区四区中,其中有两个区的单车乱停乱放数量超过标准,在“大美上饶”活动中,检查组随机抽取两个区调查单车乱停乱放数量,![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
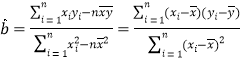 ,
,![]() ,
,
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<![]() )的图象如图所示.
)的图象如图所示.
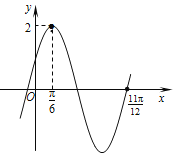
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[-![]() ,0],求函数f(x)的值域.
,0],求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com