
已知两点 和
和 ,若直线上存在点P,使
,若直线上存在点P,使 ,则称该直线为“B型直线”.给出下列直线:①
,则称该直线为“B型直线”.给出下列直线:①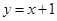 ;②
;② ;③
;③ ;④
;④ ,其中为“B型直线”的是( )
,其中为“B型直线”的是( )
A.①③ B.①② C.③④ D.①④
B
【解析】
试题分析:∵|PM|-|PN|=6∴点P在以M、N为焦点的双曲线的右支上,即 (x>0),①
(x>0),①
,把y=x+1代入双曲线 (x>0)并整理,得7x2-18x-153=0,∵△=(-18)2-4×7×(-153)>0∴y=x+1是“B型直线”.
(x>0)并整理,得7x2-18x-153=0,∵△=(-18)2-4×7×(-153)>0∴y=x+1是“B型直线”.
②把y=2代入双曲线
 (x>0)并整理,得x2=
(x>0)并整理,得x2= ,∴y=2是“B型直线”.
,∴y=2是“B型直线”.
③把 代入双曲线
代入双曲线 (x>0)并整理,得144=0,不成立.∴
(x>0)并整理,得144=0,不成立.∴ 不是“B型直线”。④把y=2x+1代入双曲线
不是“B型直线”。④把y=2x+1代入双曲线
 (x>0)并整理,得20x2+36x+153=0,∵△=362-4×20×153<0∴y=2x+1不是“B型直线”.
(x>0)并整理,得20x2+36x+153=0,∵△=362-4×20×153<0∴y=2x+1不是“B型直线”.
故选B。
考点:本题主要考查曲线方程的概念,双曲线的定义及标准方程。
点评:创新题型,理解满足 。的点是双曲线
。的点是双曲线 右支上的点是关键。
右支上的点是关键。


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
(本小题满分12分) 已知两点![]() 和
和![]() 分别在直线
分别在直线![]() 和
和![]()
![]() 上运动,且
上运动,且![]() ,动点
,动点![]() 满足:
满足:![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹记为曲线
的轨迹记为曲线![]() . (Ⅰ)求曲线
. (Ⅰ)求曲线![]() 的方程,并讨论曲线
的方程,并讨论曲线![]() 的类型; (Ⅱ)过点
的类型; (Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,若对于任意
,若对于任意![]() ,都有
,都有![]() 为锐角,求直线
为锐角,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两点![]() 和
和![]() 分别在直线
分别在直线![]() 和
和![]() 上运动,且
上运动,且![]() ,动点满足:
,动点满足:![]() 为坐标原点),点的轨迹记为曲线
为坐标原点),点的轨迹记为曲线![]()
(1)求曲线![]() 的方程,并讨论曲线
的方程,并讨论曲线![]() 的类型;
的类型;
(2)过点(0,1)作直线![]() 与曲线。交于不同的两点、,若对于任意
与曲线。交于不同的两点、,若对于任意![]() ,都有
,都有![]() 为锐角,求直线
为锐角,求直线![]() 的斜率
的斜率![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:山东省烟台市开发区高中2010届高三10月月考(理) 题型:解答题
已知两点 和
和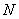 分别在直线
分别在直线 和
和 上运动,且
上运动,且 ,动点
,动点 满足:
满足: 为坐标原点),点
为坐标原点),点 的轨迹记为曲线
的轨迹记为曲线
(1)求曲线 的方程,并讨论曲线
的方程,并讨论曲线 的类型;
的类型;
(2)过点(0,1)作直线 与曲线。交于不同的两点
与曲线。交于不同的两点 、
、 ,若对于任意
,若对于任意 ,都有
,都有 为锐角,求直线
为锐角,求直线 的斜率
的斜率 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com