
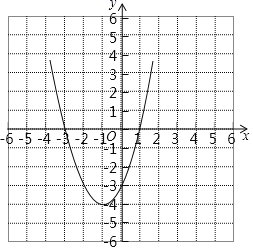
【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .
【答案】(1)0;(2)图象见解析;(3)![]() 或
或![]() (4)
(4)![]() .
.
【解析】
(1)先确定出对称轴,根据抛物线的对称性即可求得;
(2)根据二次函数图象的画法作出图象即可;
(3)根据抛物线的对称性,(-4,5)关于直线x=-1的对称点是(2,5),根据图象即可求得结论,
(4)根据函数图象,写y的取值范围即可.
(1)由图表,根据抛物线的对称性,可知抛物线的顶点坐标为![]() ,
,
所以抛物线的对称轴的方程为![]() ,
,
又由![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() ,所以
,所以![]() .
.
(2)函数图象如图所示;
(3)因为![]() 关于直线x=-1的对称点是
关于直线x=-1的对称点是![]() ,
,
由图象可知当![]() 时,x的取值范围是
时,x的取值范围是![]() 或
或![]() ,
,
即x的取值范围是![]() 或
或![]() .
.
(4)由图表可知,当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
结合图象可知当![]() 时,y的取值范围是
时,y的取值范围是![]() ,
,
即y的取值范围是![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]
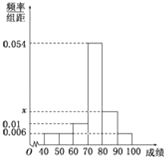
(Ⅰ)求图中![]() 的值,并估计该班期中考试数学成绩的众数;
的值,并估计该班期中考试数学成绩的众数;
(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-mlnx,h(x)=x2-x+a.
(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在区间(1,3)上恰有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,要推进绿色发展,倡导“简约知适度、绿色低碳”的生活方式,开展创建“低碳生活,绿色出行”等行动.在这一号召下,越来越多的人秉承“能走不骑,能骑不坐,能坐不开”的出行理念,尽可能采取乘坐公交车骑自行车或步行等方式出行,减少交通拥堵,共建清洁、畅通高效的城市生活环境.某市环保机构随机抽查统计了该市部分成年市民某月骑车次数,统计如下:
人数 年龄 |
|
|
|
|
|
|
18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
60岁及以上 | 25 | 10 | 10 | 19 | 4 | 2 |
联合国世界卫生组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.
(I)若从被抽查的该月骑车次数在![]() 的老年人中随机选出两名幸运者给予奖励,求其中一名幸运者该月骑车次数在
的老年人中随机选出两名幸运者给予奖励,求其中一名幸运者该月骑车次数在![]() 之间,另一名幸运者该月骑车次数在
之间,另一名幸运者该月骑车次数在![]() 之间的概率;
之间的概率;
(Ⅱ)用样本估计总体的思想,解决如下问题:
(![]() )估计该市在32岁至44岁年龄段的一个青年人每月骑车的平均次数;
)估计该市在32岁至44岁年龄段的一个青年人每月骑车的平均次数;
(![]() ) 若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
) 若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角E-BF-C的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com