
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:中位数为2,极差为5; 乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0; 丁地:总体平均数为2,总体方差为3.
A.甲地B.乙地C.丙地D.丁地
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推.排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推.已知2018年为戊戌年,那么到改革开放一百年,即2078年为__________年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,点P(0,1).
,点P(0,1).
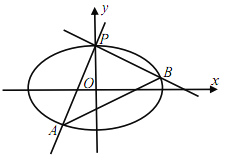
(1)过P点作斜率为k(k>0)的直线交椭圆C于A点,求弦长|PA|(用k表示);
(2)过点P作两条互相垂直的直线PA,PB,分别与椭圆交于A、B两点,试问:直线AB是否经过一定点?若存在,则求出定点,若不存在,则说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
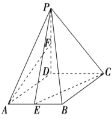
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
A. 3690 B. 3660 C. 1845 D. 1830
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是![]() .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com