
【题目】已知函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
(1) 求![]() 的解析式;
的解析式;
(2) 求过点![]() 的切线方程.
的切线方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 处的切线的斜率为
处的切线的斜率为![]() ,求出导函数,可得
,求出导函数,可得![]() 是
是![]() 的两根,且
的两根,且![]() ,解方程组即可求得
,解方程组即可求得![]() 的值,从而求得
的值,从而求得![]() 的解析式;(2)设切点,求切线方程,将点
的解析式;(2)设切点,求切线方程,将点![]() 切线方程得到
切线方程得到![]() ,解方程可得
,解方程可得![]() ,从可得切线斜率,运用点斜式方程,进而得到所求切线的方程.
,从可得切线斜率,运用点斜式方程,进而得到所求切线的方程.
试题解析:(1)函数f(x)=ax3+bx2+cx的导数为f'(x)=3ax2+2bx+c, 依题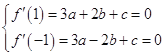 ,
,
又f'(0)=﹣3即c=﹣3 ∴a=1,b=0, ∴f(x)=x3﹣3x
(2)解:设切点为(x0 , x03﹣3x0), ∵f'(x)=3x2﹣3∴切线的斜率为f'(x0)=3x02﹣3,∴切线方程为y﹣(x03﹣3x0)=(3x02﹣3)(x﹣x0),
又切线过点A(2,2),
∴2﹣(x03﹣3x0)=(3x02﹣3)(2﹣x0),
∴2x03﹣6x02+8=0,即为2(x0+1)(x0﹣2)2=0, 解得x0=﹣1或2,
可得过点A(2,2)的切线斜率为0或9,
即有过点A(2,2)的切线方程为y﹣2=0或y﹣2=9(x﹣2),
即为y﹣2=0或9x﹣y﹣16=0 .


科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-ax+a2-13=0},B={x|x2-4x+3=0},C={x|x2—3x=0}.
(1)若A∩B=A![]() B,求a的值;
B,求a的值;
(2)若![]() ,
,![]() 求a的值.
求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB. 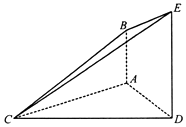
(I)求证:平面BCE⊥平面CDE;
(II)求平面BCE与平面ADEB所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程为![]() (α为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(α为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(1)写出圆C的极坐标方程及圆心C的极坐标;
(2)直线l的极坐标方程为![]() 与圆C交于M,N两点,求△CMN的面积.
与圆C交于M,N两点,求△CMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=2an+1(n∈N*).
(1)求数列{an}的通项公式;
(2)设Sn为数列{ ![]() }的前n项和,求证:1≤Sn<4.
}的前n项和,求证:1≤Sn<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣2|x﹣a|,a>0. (Ⅰ)当a=1时,求不等式f(x)>1的解集;
(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() .
.![]() 交于
交于![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:

①平面![]()
![]() 平面
平面![]() ;②当且仅当
;②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小; ③四边形
的面积最小; ③四边形![]() 周长
周长![]() ,
,![]() 是单调函数;④四棱锥
是单调函数;④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
以上命题中真命题的序号为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com