
(本题满分14分)设数列 的前
的前 项和为
项和为 ,且满足
,且满足 (
( =1,2,3,…).
=1,2,3,…).
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(1)  ; (2)
; (2)  。
。
【解析】
试题分析:(Ⅰ)由题设知a1=1,an+Sn=2,an+1+Sn+1=2,两式相减:an+1-an+an+1=0,故有2an+1=an,,n∈N+,由此能求出数列{an}的通项公式.
(Ⅱ)由bn+1=bn+an(n=1,2,3,…),知bn+1-bn=( )n-1,再由累加法能推导出bn=3-2(
)n-1,再由累加法能推导出bn=3-2(  )n-1(n=1,2,3,…).
)n-1(n=1,2,3,…).
解:(1)当 时,
时, ,则
,则 ---------------2分
---------------2分
当 时
,
时
,
 ,
,
则
 --------------------------------4分
--------------------------------4分
所以,数列 是以首项
是以首项 ,公比为
,公比为 的等比数列,从而
的等比数列,从而 ----8分
----8分
(2)


当 时,
时,
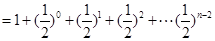 --10分
--10分

 -----------12分
-----------12分
又 满足,
满足,
 ---------14分
---------14分
考点:本试题主要第(Ⅰ)题考查迭代法求数列通项公式的方法,第(Ⅱ)题考查累加法求数列通项公式的方法。
点评:解决该试题的关键是能够利用迭代法表示出通项公式的运用,寻找规律,以及根据列加法求解数列的通项公式的问题。


科目:高中数学 来源: 题型:
(本题满分14分)
设函数![]() ,
,![]() 。
。
(1)若![]() ,过两点
,过两点![]() 和
和![]() 的中点作
的中点作![]() 轴的垂线交曲线
轴的垂线交曲线![]() 于点
于点![]() ,求证:曲线
,求证:曲线![]() 在点
在点![]() 处的切线
处的切线![]() 过点
过点![]() ;
;
(2)若![]() ,当
,当![]() 时
时![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011——2012学年湖北省洪湖二中高三八月份月考试卷理科数学 题型:解答题
(本题满分14分)设椭圆 的左、右焦点分别为F1与
的左、右焦点分别为F1与
F2,直线 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。
(1)求椭圆C的方程;
(2)设椭圆C经过伸缩变换 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 相切
相切
且与椭圆C交于不同的两点A、B,若 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷三 题型:解答题
(本题满分14分)设M是由满足下列条件的函数 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 ”
”
(I)证明:函数 是集合M中的元素;
是集合M中的元素;
(II)证明:函数 具有下面的性质:对于任意
具有下面的性质:对于任意
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省揭阳市高三调研检测数学理卷 题型:解答题
本题满分14分)
设函数 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,试确定
,试确定 的单调性;
的单调性;
(3)记 ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com