
已知异面直线
l1和l2,l1⊥l2,MN是l1和l2的公垂线,MN=4,A∈l1,B∈l2,AM=BN=2,O是MN中点.①求
l1与OB的成角.②求
A点到OB距离.|
解析:(1)如图,画两个相连的正方体,将题目条件一一标在图中.
OB在底面上射影NB⊥CD,由三垂线定理,OB⊥CD,又CD∥MA, ∴ OB⊥MA即OB与l1成90°(2)连结BO并延长交上底面于E点. ME=BN, ∴ ME=2,又ON=2∴ 作 AQ⊥BE,连结MQ.对于平面 EMO而言,AM、AQ、MQ分别为垂线、斜线、斜线在平面内的射影,由三垂线逆定理得MQ⊥EO.在 Rt△MEO中,评述:又在 Rt△AMQ中,
分析:本题若将条件放入立方体的“原型”中,抓住“一个平面四条线”的图形特征及“直线平面垂直”的关键性条件,问题就显得简单明了. |


科目:高中数学 来源: 题型:
 在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4
在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕头市金山中学高一(上)期末数学试卷(解析版) 题型:解答题
 ,求直线l的方程;
,求直线l的方程;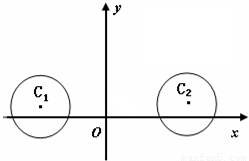
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕头市金山中学高一(上)期末数学试卷(解析版) 题型:解答题
 ,求直线l的方程;
,求直线l的方程;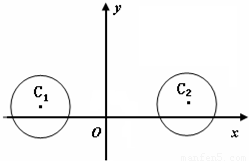
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com