
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若关于![]() 的方程
的方程![]() 有且仅有一个实根,求实数
有且仅有一个实根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递减区间是
的单调递减区间是![]() .(2)实数
.(2)实数![]() 的取值范围是
的取值范围是![]()
【解析】
(Ⅰ)求函数f(x)的导数,利用导数小于0,求解单调递减区间;
(Ⅱ)分离变量,通过函数的图象的交点个数,判断零点个数,利用单调性求解函数的极值,推出结果即可.
(Ⅰ)由题可得:![]()
令![]() ,得
,得![]() ,解得:
,解得:![]()
∴函数![]() 的单调递减区间是
的单调递减区间是![]() .
.
(Ⅱ)∵方程![]() 有且仅有一个实根
有且仅有一个实根
∴方程![]() 有且仅有一个非零实根,即方程
有且仅有一个非零实根,即方程![]() 有且仅有一个实根.
有且仅有一个实根.
因此,函数![]() 的图像与直线
的图像与直线![]() 有且仅有一个交点.
有且仅有一个交点.
结合(Ⅰ)可知,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,
,![]() .
.
∴函数![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() .
.
又∵![]() 且
且![]() 时,
时,![]() .∴当
.∴当![]() 或
或![]() 或
或![]() 时,
时,
函数![]() 的图像与直线
的图像与直线![]() 有且仅有一个交点.
有且仅有一个交点.
∴若方程![]() 有且仅有一个实根,
有且仅有一个实根,
实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”![]() 江南梅雨的点点滴滴都流润着浓洌的诗情
江南梅雨的点点滴滴都流润着浓洌的诗情![]() 每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇
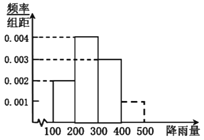
每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇![]() 年梅雨季节的降雨量
年梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
![]() Ⅰ
Ⅰ![]() “梅实初黄暮雨深”
“梅实初黄暮雨深”![]() 假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;
假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;
![]() Ⅱ
Ⅱ![]() “江南梅雨无限愁”
“江南梅雨无限愁”![]() 在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元
在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?
的期望更大?![]() 需说明理由
需说明理由![]()
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是规划的生态文旅园区,其中
区域(含边界)是规划的生态文旅园区,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为
、半径为![]() 千米.根据发展规划,要在扇形
千米.根据发展规划,要在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
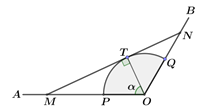
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数;
的函数;
(2)已知公路每千米的造价为![]() 万元,问建造这样一条公路
万元,问建造这样一条公路![]() ,至少要投入多少万元?
,至少要投入多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域内存在区间
在定义域内存在区间![]() ,使得该函数在区间
,使得该函数在区间![]() 上的值域为
上的值域为![]() ,则称函数
,则称函数![]() 是该定义域上的“和谐函数”.
是该定义域上的“和谐函数”.
(1)判断函数![]() 是不是“和谐函数”,并说明理由;
是不是“和谐函数”,并说明理由;
(2)若函数![]() 是“和谐函数”,求实数
是“和谐函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点.

(1)求证:DE=DA;
(2)求证:平面BDM⊥平面ECA;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com