
【题目】关于下列结论:
①函数![]() 是偶函数;
是偶函数;
②直线![]() 是函数
是函数![]() 的图象的一条对称轴;
的图象的一条对称轴;
③将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,所得图象的函数解析式为
个单位后,所得图象的函数解析式为![]() ;
;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称.
成中心对称.
其中所有正确结论的序号为______.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是______.
①若直线![]() 与直线
与直线![]() 互相垂直,则
互相垂直,则![]()
②若![]() ,
,![]() 两点到直线
两点到直线![]() 的距离分别是
的距离分别是![]() ,
,![]() ,则满足条件的直线
,则满足条件的直线![]() 共有3条
共有3条
③过![]() ,
,![]() 两点的所有直线方程可表示为
两点的所有直线方程可表示为![]()
④经过点![]() 且在
且在![]() 轴和
轴和![]() 轴上截距都相等的直线方程为
轴上截距都相等的直线方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①底面是矩形的平行六面体是长方体;
②棱长都相等的直四棱柱是正方体;
③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;
④相邻两个面垂直于底面的棱柱是直棱柱;
⑤各侧面是全等的等腰三角形的棱锥一定是正棱锥;
⑥三棱锥的顶点在底面上的射影是底面三角形的垂心,则这个棱锥的三条侧棱长相等.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() ,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积与上一年剩余面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是( )
A. 若![]() 为真命题,则
为真命题,则![]() 中至少有一个为真命题.
中至少有一个为真命题.
B. 命题:“若![]() 是幂函数,则
是幂函数,则![]() 的图象不经过第四象限”的否命题是假命题.
的图象不经过第四象限”的否命题是假命题.
C. 命题“![]() ,有
,有![]() 且
且![]() ”的否定形式是“
”的否定形式是“![]() ,有
,有![]() 且
且![]() ”.
”.
D. 若直线![]() 和平面
和平面![]() ,满足
,满足![]() .则“
.则“![]() ” 是“
” 是“![]() ”的充分不必要条件.
”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD所在的平面与等腰梯形ABEF所在的平面互相垂直,AB∥CD∥EF,AB⊥AD,CD=DA=AF=FE=2,AB=4.
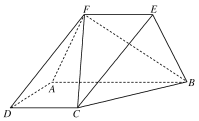
(1)求证:DF∥平面BCE;
(2)求二面角C—BF—A的正弦值;
(3)线段CE上是否存在点G,使得AG⊥平面BCF?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x∈[-1,1],函数
,x∈[-1,1],函数![]() ,a∈R的最小值为h(a).
,a∈R的最小值为h(a).
(1)求h(a)的解析式;
(2)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com