
【题目】对于集合![]() ,
,![]() ,
,![]() ,
,![]() .集合
.集合![]() 中的元素个数记为
中的元素个数记为![]() .规定:若集合
.规定:若集合![]() 满足
满足![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)已知集合![]() ,
,![]() ,写出
,写出![]() ,
,![]() 的值;
的值;
(II)已知集合![]() ,
,![]() 为等比数列,
为等比数列,![]() ,且公比为
,且公比为![]() ,证明:
,证明:![]() 具有性质
具有性质![]() ;
;
(III)已知![]() 均有性质
均有性质![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(I)![]() ; (II)见解析; (III)
; (II)见解析; (III)![]() .
.
【解析】
(Ⅰ)分别求得A+A,B+B,然后可得![]() ,
,![]() 的值;
的值;
(Ⅱ)将原问题进行等价变形,然后利用反证法证明题中的结论即可;
(Ⅲ)原问题等价于任意两个元素之和均不相同,且任意两个不同元素之差的绝对值均不相同.据此整理计算即可确定![]() 的最小值.
的最小值.
(I)由题意可得:![]() ,
,![]() ,
,
故![]()
(II)要证![]() 具有性质
具有性质![]() ,只需证明,若
,只需证明,若![]() ,则
,则![]() .
.
假设上式结论不成立,即若![]() ,则
,则![]() .
.
即![]() ,即
,即![]() ,
,
![]() ,
,![]() .
.
因为上式的右边为![]() 的倍数,而上式的左边为
的倍数,而上式的左边为![]() 的倍数,所以上式不成立.
的倍数,所以上式不成立.
故假设不成立,原命题成立.
(III)由题意,集合![]() 具有性质
具有性质![]() ,等价于任意两个元素之和均不相同.
,等价于任意两个元素之和均不相同.
如,对于任意的![]() ,有
,有![]() ,
,
等价于![]() ,即任意两个不同元素之差的绝对值均不相同.
,即任意两个不同元素之差的绝对值均不相同.
令![]() ,
,
所以![]() 具有性质
具有性质![]()
![]() .
.
因为集合![]() 均有性质
均有性质![]() ,且
,且![]() ,
,
所以![]()
![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
所以![]() 的最小值为
的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: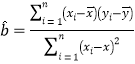 ,
,![]() ;
;![]() ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两位同学整理了某学科高三以来9次考试的成绩(甲缺席了其中3次考试,只有6次成绩),得到如下茎叶图.
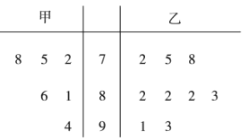
(1)若用分层抽样的方法从两人的15个成绩选取5个评估,应选取甲的几次成绩?若分层抽样时对甲的成绩采用随机抽取,求选取到的甲的成绩至少有一次高于85分的概率;
(2)试通过表中的所有数据,从平均水平和稳定性来评判两位同学该学科的考试成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在区间[-c,c]上的奇函数,其图象如下图所示.令g(x)=af(x)+b,则下列关于函数g(x)的结论:
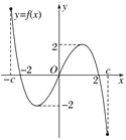
①若a<0,则函数g(x)的图象关于原点对称;
②若a=-1,-2<b<0,则方程g(x)=0有大于2的实根;
③若a≠0,b=2,则方程g(x)=0有两个实根;
④若a≠0,b=2,则方程g(x)=0有三个实根.
其中,正确的结论为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】货车欲以xkm/h的速度行驶,去130km远的某地,按交通法规,限制x的允许范围是50≤x≤100,假设汽油的价格为2元/升,而汽车耗油的速率是![]() 升/小时.司机的工资是14元/小时,试问最经济的车速是多少?这次行车往返的总费用最低是多少?
升/小时.司机的工资是14元/小时,试问最经济的车速是多少?这次行车往返的总费用最低是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com