
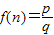 .如
.如 .以下有关
.以下有关 的说法中,正确的个数为( )
的说法中,正确的个数为( ) ;
;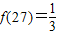 ;
;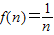 ;
; 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| p |
| q |
| 3 |
| 4 |
| 1 |
| 7 |
| 3 |
| 8 |
| 4 |
| 7 |
| 9 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| p |
| q |
| 3 |
| 4 |
| p |
| q |
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| n |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三第二次段考文科数学试卷(解析版) 题型:填空题
将正整数12分解成两个正整数的乘积有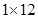 ,
,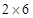 ,
,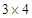 三种,其中
三种,其中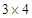 是这三种分解中,两数差的绝对值最小的,我们称
是这三种分解中,两数差的绝对值最小的,我们称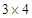 为12的最佳分解.当
为12的最佳分解.当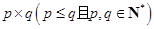 是正整数
是正整数 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数 ,例如
,例如 .关于函数
.关于函数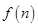 有下列叙述: ①
有下列叙述: ① ,②
,② ,③
,③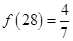 ,④
,④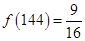 .其中正确的序号为 (填入所有正确的序号).
.其中正确的序号为 (填入所有正确的序号).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市毕业班综合测试数学理科试题 题型:填空题
将正整数12分解成两个正整数的乘积有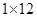 ,
,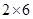 ,
,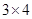 三种,其中
三种,其中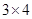 是这三种分解中,两数差的绝对值最小的,我们称
是这三种分解中,两数差的绝对值最小的,我们称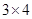 为12的最佳分解.当
为12的最佳分解.当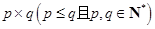 是正整数
是正整数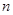 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数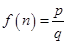 ,例如
,例如 .
.
关于函数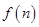 有下列叙述:①
有下列叙述:①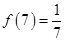 ,②
,② ,③
,③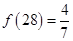 ,④
,④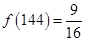 .其中正确的序号为 (填入所有正确的序号).
.其中正确的序号为 (填入所有正确的序号).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高二(下)期中数学试卷(文科)(解析版) 题型:选择题
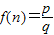 .如
.如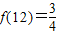 .以下有关
.以下有关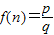 的说法中,正确的个数为( )
的说法中,正确的个数为( )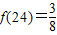 ;
;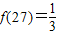 ;
;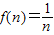 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com