
【题目】下列判断正确的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
B.已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
C.若随机变量![]() 服从二项分布:
服从二项分布:![]() ,则
,则![]() ;
;
D.已知直线![]() 经过点
经过点![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】为了了解某市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:![]() ,并绘制出频率分布直方图,如图所示.
,并绘制出频率分布直方图,如图所示.

(1)求频率分布直方图中![]() 的值,并估计该市高中学生的平均成绩;
的值,并估计该市高中学生的平均成绩;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 四名学生的考试成绩在区间
四名学生的考试成绩在区间![]() 内,
内,![]() 、
、![]() 两名学生的考试成绩在区间
两名学生的考试成绩在区间![]() 内,现从这6名学生中任选两人参加座谈会,求学生
内,现从这6名学生中任选两人参加座谈会,求学生![]() 、
、![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角三角形ABC中,![]() ,
,![]() (如右图所示)
(如右图所示)
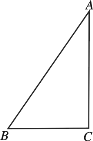
(Ⅰ)若以AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.
(Ⅱ)一只蚂蚁在问题(Ⅰ)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥M-ABC中,MA=MB=MC=AC=![]() ,AB=BC=2,O为AC的中点,点N在边BC上,且
,AB=BC=2,O为AC的中点,点N在边BC上,且![]() .
.
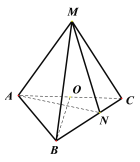
(1)证明:BO![]() 平面AMC;
平面AMC;
(2)求二面角N-AM-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
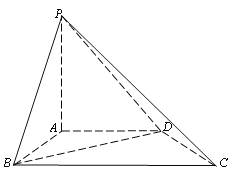
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用 (基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费
元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费![]() 基准保费
基准保费![]() (
(![]() 浮动比率
浮动比率![]() ).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:
).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:

某机构为了研究某一品牌普通6座以下私家车的投保情况,为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数,得到下面的柱状图:
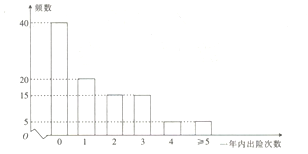
已知小明家里有一辆该品牌普通6座以下私家车且需要续保,续保费用为![]() 元.
元.
(1)记![]() 为事件“
为事件“![]() ”,求
”,求![]() 的估计值;
的估计值;
(2)求![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长为a,b,c,有下列四个命题:
的三边长为a,b,c,有下列四个命题:
①以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
②以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
③以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
④以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在.
为边长的三角形一定存在.
其中正确的是( )
A.①③B.②③C.②④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com