
【题目】已知定义在R上的函数f(x)=x3+(k-1)x2+(k+5)x-1.
(1)若k=-5,求f(x)的极值;
(2)若f(x)在区间(0,3)内单调,求实数k的取值范围.
【答案】(1)f(x)极大值是f(0)=-1,f(x)极小值是f(4)=-33;
(2)![]()
【解析】
(1)代入k的值,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,即可求出函数的极值;
(2)求出函数的导数,通过讨论对称轴的范围,得到函数的单调区间,从而确定k的范围即可.
解:(1)k=-5时,f(x)=x3-6x2-1,
f′(x)=3x2-12x,
令f′(x)>0,解得:x>4或x<0,
令f′(x)<0,解得:0<x<4,
故f(x)在(-∞,0)递增,在(0,4)递减,在(4,+∞)递增,
故x=0时,f(x)取极大值,且极大值是f(0)=-1,
x=4时,f(x)取极小值,且极小值是f(4)=-33;
(2)f′(x)=3x2+2(k-1)x+k+5=3![]() -
-![]() +k+5,
+k+5,
f′(x)的图象是开口向上的抛物线,对称轴是直线x=![]() ,
,
①当![]() ≤0即k≥1时,f′(0)=k+5>0且f′(x)在(0,3)递增,
≤0即k≥1时,f′(0)=k+5>0且f′(x)在(0,3)递增,
故f′(x)>0在(0,3)内恒成立,
故f(x)在(0,3)递增,即k≥1时满足题意;
②当![]() ≥3即k≤-8时,f′(0)=k+5<0且f′(x)在(0,3)递减,
≥3即k≤-8时,f′(0)=k+5<0且f′(x)在(0,3)递减,
故f′(x)<0在(0,3)内恒成立,
故f(x)在(0,3)内递减,即k≤-8满足题意;
③当0<![]() <3即-8<k<1时,
<3即-8<k<1时,
(ⅰ)若-8<k≤-5,则f′(0)=k+5≤0,
只需f′(3)=7k+26≤0即k≤ -![]() ,
,
此时f′(x)≤0在(0,3)内恒成立,
即f(x)在(0,3)递减,
(ⅱ)若-5<k<1,则f′(0)=k+5>0,
此时只需f′(![]() )=-
)=-![]() +k+5≥0,
+k+5≥0,
解得:![]()
即-2≤k<1时,f′(x)≥0在(0,3)内恒成立,
即-2≤k<1时,f(x)在(0,3)递增,
综上,若f(x)在区间(0,3)内单调,实数k的范围是(-∞,-5]∪[-2,+∞).


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】(2016·山东卷)已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.
(1)求数列{bn}的通项公式;
(2)令cn=![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.在![]() 中,若
中,若![]() ,则
,则![]()
B.在锐角三角形![]() 中,不等式
中,不等式![]() 恒成立
恒成立
C.在![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() 为等腰直角三角形
为等腰直角三角形
D.在![]() 中,若
中,若![]() ,
,![]() ,三角形面积
,三角形面积![]() ,则三角形外接圆半径为
,则三角形外接圆半径为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面ADEF,其中四边形ABCD为矩形,四边形ADEF为梯形,AF∥DE,AF⊥EF,AF=AD=2AB=2DE=2.
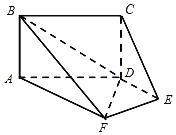
(1)求证:CE∥面ABF;
(2)求直线DE与平面BDF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() 两点.
两点.
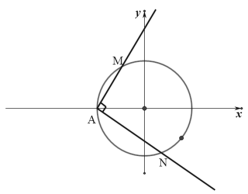
(1)过点![]()
![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() ;
;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点
过定点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com