
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线PA交x轴于点M.
,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线PA交x轴于点M.
(1)求椭圆C的方程,并求点M的坐标(用m,n表示);
(2)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.
【答案】(1)M![]() .;(2)点Q的坐标为(0,
.;(2)点Q的坐标为(0, ![]() )或(0,-
)或(0,- ![]() ).
).
【解析】试题分析:(1)根据椭圆的几何性质得出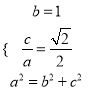 ,求解即可.
,求解即可.
(2)讲问题转化为方程![]() =|xM||xN|,求坐标即可.
=|xM||xN|,求坐标即可.
试题解析:
(1)由题意得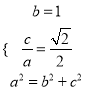 解得a2=2,故椭圆C的方程为
解得a2=2,故椭圆C的方程为![]() +y2=1.
+y2=1.
设M(xM,0).因为m≠0,所以-1<n<1.直线PA的方程为y-1=![]() x.
x.
所以xM=![]() ,即M
,即M![]() .
.
(2)因为点B与点A关于x轴对称,所以B(m,-n).
设N(xN,0),则xN=![]() .“存在点Q(0,yQ)使得∠OQM=∠ONQ”,等价于“存在点Q(0,yQ)使得
.“存在点Q(0,yQ)使得∠OQM=∠ONQ”,等价于“存在点Q(0,yQ)使得![]() ”,即yQ满足
”,即yQ满足![]() =|xM||xN|.
=|xM||xN|.
因为xM=![]() ,xN=
,xN=![]() ,
, ![]() +n2=1.
+n2=1.
所以![]() =|xM||xN|=
=|xM||xN|=![]() =2.所以yQ=
=2.所以yQ=![]() 或yQ=-
或yQ=-![]() .
.
故在y轴上存在点Q,使得∠OQM=∠ONQ,点Q的坐标为(0, ![]() )或(0,-
)或(0,- ![]() ).
).


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={![]() };②M={(x,y)|y=sinx+1};
};②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};④M={(x,y)|y=ex﹣2}.
其中是“垂直对点集”的序号是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对![]() 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共![]() 道题,答题情况如下表:
道题,答题情况如下表:
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租车司机答对题目大于等于![]() ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(II)从答对题目数小于![]() 的出租车司机中选出
的出租车司机中选出![]() 人做进一步的调查,求选出的
人做进一步的调查,求选出的![]() 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设铁路![]() 长为
长为![]() ,且
,且![]() ,为将货物从
,为将货物从![]() 运往
运往![]() ,现在
,现在![]() 上的距点
上的距点![]() 为
为![]() 的点
的点![]() 处修一公路至
处修一公路至![]() ,已知单位距离的铁路运费为
,已知单位距离的铁路运费为![]() ,公路运费为
,公路运费为![]() .
.
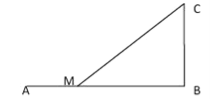
(1)将总运费![]() 表示为
表示为![]() 的函数;
的函数;
(2)如何选点![]() 才使总运费最小?
才使总运费最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为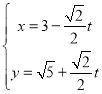 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有些家用电器(如冰箱等)使用了氟化物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量呈指数型函数变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.0025t,其中Q0是臭氧的初始量.
(1)随着时间t的增加,臭氧的含量是增加的还是减少的?
(2)试估计多少年以后将会有一半的臭氧消失?(参考数据:ln 0.5=-0.69)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com