
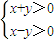 表示的平面区域为D、区域D内的动点P到直线x+y=0和直线x-y=0的距离之积为1.记点P的轨迹为曲线C、
表示的平面区域为D、区域D内的动点P到直线x+y=0和直线x-y=0的距离之积为1.记点P的轨迹为曲线C、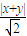 ×
× =1,整理得|x2-y2|=2.根据P∈D推断出x+y>0,x-y>0,进而可得x2-y2>0,答案可得.
=1,整理得|x2-y2|=2.根据P∈D推断出x+y>0,x-y>0,进而可得x2-y2>0,答案可得. |AB|=
|AB|=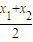 .进而根据双曲线定义得|AB|=|AF|+|BF|,进而求得x1+x2的值,求得线段AB的长.
.进而根据双曲线定义得|AB|=|AF|+|BF|,进而求得x1+x2的值,求得线段AB的长. 解:(Ⅰ)由题意可知,平面区域D如图阴影所示.
解:(Ⅰ)由题意可知,平面区域D如图阴影所示.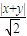 ×
×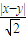 =1,
=1,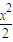 -
-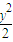 =1(x>0).
=1(x>0).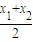 ,
,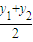 ),
), |AB|=
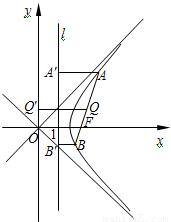
|AB|=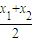 .
.
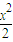 -
-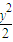 =1(x>0),
=1(x>0),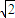 .
.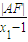 =
=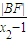 =
=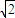 ,
,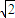 (x1-1)+
(x1-1)+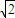 (x2-1)=
(x2-1)= (x1+x2)-2
(x1+x2)-2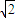 .②
.② (x1+x2)-2
(x1+x2)-2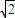 .
.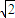 .
. .
.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(二)理数学卷(解析版) 题型:选择题
设不等式组  表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上存在区域D上的点,则a 的取值范围是 ( )
的图像上存在区域D上的点,则a 的取值范围是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013届新课标高三配套第四次月考文科数学试卷(解析版) 题型:选择题
设不等式组 表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
A. 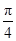 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三上学期第一次月考数学卷 题型:选择题
设不等式组  表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上存在区域D上的点,则a 的取值范围是
( )
的图像上存在区域D上的点,则a 的取值范围是
( )
A.
 B.
B.
 C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(北京卷)解析版(理) 题型:本大题
设不等式组 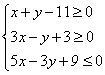 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上
的图像上
存在区域D上的点,则a 的取值范围是
(A)(1,3]
(B )[2,3] (C )
(1,2] (D )[ 3,  ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com