
(13分) (理科)已知双曲线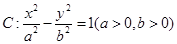 与椭圆
与椭圆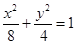 有公共焦点,且以抛物线
有公共焦点,且以抛物线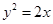 的准线为双曲线
的准线为双曲线 的一条准线.动直线
的一条准线.动直线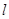 过双曲线
过双曲线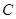 的右焦点
的右焦点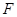 且与双曲线的右支交于
且与双曲线的右支交于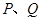 两点.
两点.
(1)求双曲线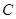 的方程;
的方程;
(2)无论直线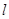 绕点
绕点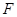 怎样转动,在双曲线
怎样转动,在双曲线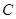 上是否总存在定点
上是否总存在定点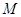 ,使
,使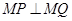 恒成立?若存在,求出点
恒成立?若存在,求出点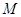 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(1)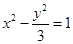
(2)双曲线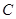 上存在定点
上存在定点 ,使
,使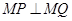 恒成立
恒成立
【解析】(理科)解:(1)设 ,则由题意有:
,则由题意有:
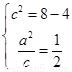 ∴
∴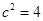 ,
,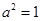 ,
,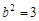
故双曲线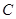 的方程为
的方程为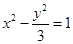 ,
…………… 4分
,
…………… 4分
(2)解法一:由(1)得点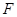 为
为
当直线l的斜率存在时,设直线方程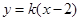 ,
,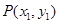 ,
,
将方程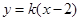 与双曲线方程联立消去
与双曲线方程联立消去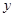 得:
得: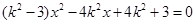 ,
,
∴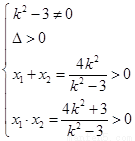 解得
解得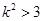 …………… 6分
…………… 6分
假设双曲线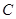 上存在定点
上存在定点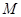 ,使
,使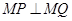 恒成立,设为
恒成立,设为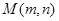
则: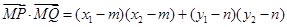
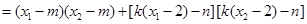
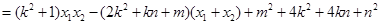
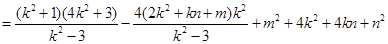
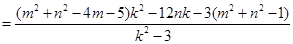
∵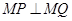 ,∴
,∴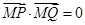 ,
,
故得: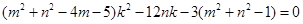 对任意的
对任意的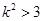 恒成立,
恒成立,
∴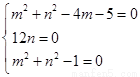 ,解得
,解得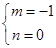
∴当点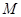 为
为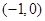 时,
时,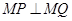 恒成立;
…………… 10分
恒成立;
…………… 10分
当直线l的斜率不存在时,由 ,
,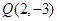 知点
知点 使得
使得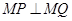 也成立.
也成立.
又因为点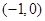 是双曲线
是双曲线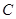 的左顶点,
…………… 12分
的左顶点,
…………… 12分
所以双曲线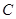 上存在定点
上存在定点 ,使
,使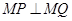 恒成立. ……………
13分
恒成立. ……………
13分
解法二(略解):当直线l的斜率不存在时,由 ,
,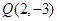 ,
,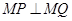 ,且点
,且点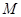 在双曲线
在双曲线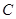 上可求得
上可求得 ,
,
当直线l的斜率存在时,将 ,
,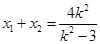 ,
,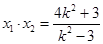 代入
代入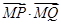 ,经计算发现
,经计算发现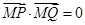 对任意的
对任意的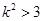 恒成立,从而恒有
恒成立,从而恒有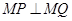 成立.
成立.
因而双曲线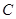 上存在定点
上存在定点 ,使
,使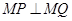 恒成立.
恒成立.


科目:高中数学 来源:2014届安徽省高一元月文理分班考试数学 题型:解答题
(13分,理科做)已知函数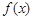 的定义域为
的定义域为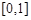 ,且同时满足:①
,且同时满足:①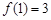 ;②
;②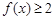 恒成立;③若
恒成立;③若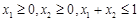 ,则有
,则有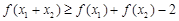 .
.
(1)试求函数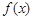 的最大值和最小值;
的最大值和最小值;
(2)试比较 与
与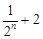 的大小
的大小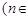 N);
N);
(3)某人发现:当x= (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1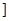 ,都有
,都有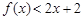 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年重庆市高二下学期期中考试数学(文) 题型:解答题
16. (本小题满分13分) 从4名文科教师和3名理科教师中任选3人担任班主任.(写出过程,最后结果用分数表示)
(1) 求所选3人都是理科教师的概率;
(2) 求所选3人中恰有1名理科教师的概率;
(3) 求所选3人中至少有1名理科教师的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
(Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;
 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;
(Ⅲ)求三棱锥M-OBC的体积(理科做,文科不做)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三第五次阶段考试理科数学试卷(解析版) 题型:解答题
某校从参加高三年级理科综合物理考试的学生中随机抽出 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中随机抽取
名学生中随机抽取 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记 分,在
分,在 记
记 分,
分,
在 记
记 分,用
分,用 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求 的分布列和数学期望.
的分布列和数学期望.

【解析】(1)中利用直方图中面积和为1,可以求解得到分数在 内的频率为
内的频率为
(2)中结合平均值可以得到平均分为:
(3)中用 表示抽取结束后的总记分x, 学生成绩在
表示抽取结束后的总记分x, 学生成绩在 的有
的有 人,在
人,在 的有
的有 人,在
人,在 的有
的有 人,结合古典概型的概率公式求解得到。
人,结合古典概型的概率公式求解得到。
(Ⅰ)设分数在 内的频率为
内的频率为 ,根据频率分布直方图,则有
,根据频率分布直方图,则有 ,可得
,可得 ,所以频率分布直方图如右图.……4分
,所以频率分布直方图如右图.……4分


(求解频率3分,画图1分)
(Ⅱ)平均分为: ……7分
……7分
(Ⅲ)学生成绩在 的有
的有 人,在
人,在 的有
的有 人,
人,
在 的有
的有 人.并且
人.并且 的可能取值是
的可能取值是 . ………8分
. ………8分
则 ;
; ;
;
 ;
;
 ;
; .(每个1分)
.(每个1分)
所以 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
…………………13分

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com