
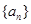 的相邻两项
的相邻两项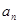 ,
,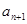 是关于
是关于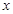 方程
方程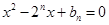 的两根,且
的两根,且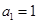 .
. 是等比数列;
是等比数列;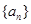 的前
的前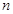 项和
项和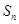 ;
;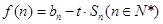 ,若
,若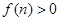 对任意的
对任意的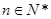 都成立,求实数
都成立,求实数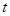 的取值范围.
的取值范围. (3)
(3)
 的递推公式:
的递推公式: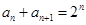 ,
,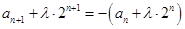 ,易求得:
,易求得: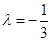 ,
,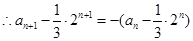 ,
,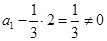 ,可知数列
,可知数列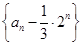 是公比为
是公比为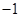 的等比数列.
的等比数列.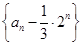 的通项公式
的通项公式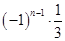 ,于是:
,于是: 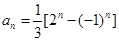 ,的拆项法,将数列
,的拆项法,将数列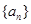 的前
的前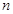 项和
项和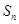 化为两个等比数列的前
化为两个等比数列的前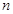 和.
和.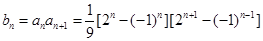 =
=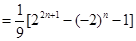
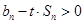 ,采用分离变量法求将求实数
,采用分离变量法求将求实数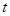 的取值范围问题,转变成求关于的函数的最值问题.
的取值范围问题,转变成求关于的函数的最值问题.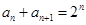 ,∴
,∴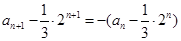 ,
,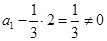 ,
,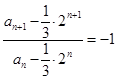 ,
,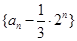 是首项为
是首项为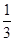 ,公比为
,公比为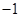 的等比数列。
的等比数列。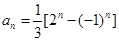 4分
4分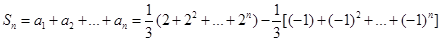 =
=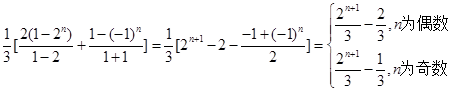 8分(注:未分奇偶写也得8分)
8分(注:未分奇偶写也得8分)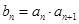 ,
,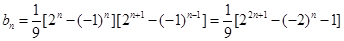 ,∴
,∴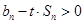 ,
,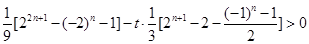 .
.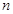 为奇数时,
为奇数时,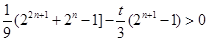 ,
,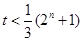 对任意的
对任意的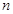 为奇数都成立,∴
为奇数都成立,∴ 。 11分
。 11分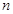 为偶数时,
为偶数时,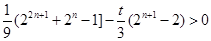 ,
,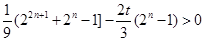 ,
,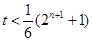 对任意的
对任意的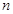 为偶数都成立,∴
为偶数都成立,∴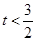 13分
13分 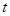 的取值范围为
的取值范围为 。 14分
。 14分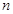 项和;3、等价转化的思想.
项和;3、等价转化的思想.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com