
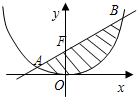
 如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).
如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).| (x1+x2)2-4x1x2 |
| ∫ | x1 x2 |
| 1 |
| 4 |
| k2+1 |
| k2+1 |
| 4 |
| 3 |
| k2+1 |
| k2+1 |
|
| (x1+x2)2-4x1x2 |
| k2+1 |
| ∫ | x2 x1 |
| 1 |
| 4 |
| x2 |
| 2 |
| 1 |
| 12 |
|
| k |
| 2 |
| 1 |
| 12 |
| k |
| 2 |
| 1 |
| 12 |
| k |
| 2 |
| 1 |
| 12 |
| k2+1 |
| k2+1 |
| 4 |
| 3 |
| k2+1 |
| k2+1 |
| 4 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |


科目:高中数学 来源: 题型:
 (2007•揭阳二模)如图,线段AB过y轴负半轴上一点M(0,a),A、B两点到y轴距离的差为2k.
(2007•揭阳二模)如图,线段AB过y轴负半轴上一点M(0,a),A、B两点到y轴距离的差为2k.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).
(2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).查看答案和解析>>
科目:高中数学 来源:《第1章 导数及其应用》2013年单元测试卷(1)(解析版) 题型:解答题
 如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).
如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).查看答案和解析>>
科目:高中数学 来源:《第1章 导数及其应用》2010年单元测试卷(二)(解析版) 题型:解答题
 如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).
如图,设由抛物线C:x2=4y与过它的焦点F的直线l所围成封闭曲面图形的面积为S(阴影部分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com