
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形![]() 的顶点在椭圆上,且对角线
的顶点在椭圆上,且对角线![]() 、
、![]() 过原点
过原点![]() ,若
,若![]() ,
,
(1)求![]() 的最值;
的最值;
(2)求证;四边形![]() 的面积为定值.
的面积为定值.
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:an+1-an=d(n∈N*),前n项和记为Sn,a1=4,S3=21.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足b1=![]() ,bn+1-bn=2an,求数列{bn}的通项公式.
,bn+1-bn=2an,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数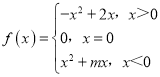 是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有
是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立,则实数a的取值范围是______.
成立,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求f(x)的定义域;
(2)当x∈(1,+∞),
①求证:f(x)在区间(1,+∞)上是减函数;
②求使关系式f(2+m)>f(2m-1)成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,
上, ![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(![]() )求椭圆
)求椭圆![]() 的离心率.
的离心率.
(![]() )当
)当![]() 边通过坐标原点
边通过坐标原点![]() 时,求
时,求![]() 的长及
的长及![]() 的面积.
的面积.
(![]() )当
)当![]() ,且斜边
,且斜边![]() 的长最大时,求
的长最大时,求![]() 所在直线的方程.
所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名大学有男生14000人,女生10000人.该校体育学院想了解本校学生的运动状况,根据性别采取分层抽样的方法从全校学生中抽取120人,统计他们平均每天运动的时间(已知该校学生平均每天运动的时间范围是![]()
![]() ),如下表所示.
),如下表所示.
男生平均每天运动的时间分布情况:

女生平均每天运动的时间分布情况:
![]()
(1)假设同组中的每个数据均可用该组区间的中间值代替,请根据样本估算该校男生平均每天运动的时间(结果精确到0.1).
(2)若规定平均每天运动的时间不少于![]() 的学生为“运动达人”,低于
的学生为“运动达人”,低于![]() 的学生为“非运动达人”.
的学生为“非运动达人”.
(ⅰ)根据样本估算该校“运动达人”的数量;
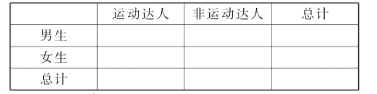
(ⅱ)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“运动达人”与性别有关.
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“运动达人”与性别有关.
参考公式:  ,其中
,其中![]() .
.
参考数据:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com