
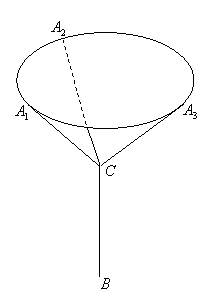
 某广场一雕塑造型结构如图所示,最上层是一呈水平状态的圆环,其半径为2m,通过金属杆BC,CA1,CA2,CA3支撑在地面B处(BC垂直于水平面),A1,A2,A3是圆环上的三等分点,圆环所在的水平面距地面10m,设金属杆CA1,CA2,CA3所在直线与圆环所在水平面所成的角都为θ.(圆环及金属杆均不计粗细)
某广场一雕塑造型结构如图所示,最上层是一呈水平状态的圆环,其半径为2m,通过金属杆BC,CA1,CA2,CA3支撑在地面B处(BC垂直于水平面),A1,A2,A3是圆环上的三等分点,圆环所在的水平面距地面10m,设金属杆CA1,CA2,CA3所在直线与圆环所在水平面所成的角都为θ.(圆环及金属杆均不计粗细)| 2 |
| cosθ |
| 6 |
| cosθ |
| 2(3-sinθ) |
| cosθ |
| π |
| 2 |
| 2(3sinθ-1) |
| cos2θ |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2n |
| cosθ |
| 2(n-sinθ) |
| cosθ |
| 2(nsinθ-1) |
| cos2θ |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| 3 |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
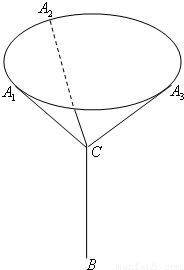
 (2012•衡阳模拟)某广场二雕塑造型结构如图所示,最上层是呈水平状态的圆环且圆心为O,其半径为2m,通过金厲杆BC,CA1,CA2,…,CAn支撑在地面B处(BC垂直于水平面).A1,A2,A3,…,An是圆环上的n等分点,圆环所在的水平面距地面1Om,设金属杆CA1,CA2,…,CAn所在直线与圆环所在水平面所成的角都为θ(圓环及金厲杆均不计粗细)
(2012•衡阳模拟)某广场二雕塑造型结构如图所示,最上层是呈水平状态的圆环且圆心为O,其半径为2m,通过金厲杆BC,CA1,CA2,…,CAn支撑在地面B处(BC垂直于水平面).A1,A2,A3,…,An是圆环上的n等分点,圆环所在的水平面距地面1Om,设金属杆CA1,CA2,…,CAn所在直线与圆环所在水平面所成的角都为θ(圓环及金厲杆均不计粗细)查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)
某广场一雕塑造型结构如图所示,最上层是一呈水平状态的圆环,其半径为![]() ,通过金属杆
,通过金属杆![]() 支撑在地面
支撑在地面![]() 处(
处(![]() 垂直于水平面),
垂直于水平面),![]() 是圆环上的三等分点,圆环所在的水平面距地面
是圆环上的三等分点,圆环所在的水平面距地面![]() ,设金属杆
,设金属杆![]() 所在直线与圆环所在水平面所成的角都为
所在直线与圆环所在水平面所成的角都为![]() 。(圆环及金属杆均不计粗细)
。(圆环及金属杆均不计粗细)
(1)当![]() 的正弦值为多少时,金属杆
的正弦值为多少时,金属杆![]() 的总长最短?
的总长最短?
 (2)为美观与安全,在圆环上设置
(2)为美观与安全,在圆环上设置![]() 个等分点,并仍按上面方法连接,若还要求金属杆
个等分点,并仍按上面方法连接,若还要求金属杆![]() 的总长最短,对比(1)中
的总长最短,对比(1)中![]() 点位置,此时
点位置,此时![]() 点将会上移还是下移,请说明理由。
点将会上移还是下移,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省省城名校高三(上)第二次联考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省扬州市高三(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com