
分析 (1)f(1)即把函数中的所有x值代为1,结合等差数列的求和公式,计算可得,同理求得f(5),f(20);
(2)设x是1~20中的某一整数,则f(x)=(x-1)+(x-2)+…+3+2+1+0+1+2+…+(20-x),再由等差数列的求和公式,结合二次函数的最值求法,注意x为整数,即可得到最小值.
解答 解:(1)由f(x)=|x-1|+|x-2|+|x-3|+…+|x-20|,
得f(1)=0+1+2+…+19=$\frac{19×(1+19)}{2}$=190;
f(5)=4+3+2+1+0+1+2+…+15=10+$\frac{15×(1+15)}{2}$=10+120=130;
f(20)=19+18+17+…+3+2+1+0=$\frac{19×(19+1)}{2}$=190.
(2)设x是1~20中的某一整数,
则f(x)=(x-1)+(x-2)+…+3+2+1+0+1+2+…+(20-x)
=$\frac{(x-1)[1+(x-1)]}{2}$+$\frac{(20-x)[1+(20-x)]}{2}$
=$\frac{1}{2}$(2x2-42x+420)=x2-21x+210=(x-$\frac{21}{2}$)2+$\frac{399}{4}$.
因为x∈N+,所以当x=10或11时,f(x)取最小值,
f(10)=f(11)=100,即最小值是100.
点评 本题主要考查函数的最值求法,注意运用等差数列的求和公式和二次函数的最值求法,考查运算能力,属于中档题.


科目:高中数学 来源:2017届江西南昌新课标高三一轮复习训练三数学试卷(解析版) 题型:解答题
已知函数
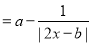 是偶函数,
是偶函数, 为实常数.
为实常数.
(1)求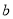 的值;
的值;
(2)当 时,是否存在
时,是否存在 ,使得函数
,使得函数 在区间
在区间 上的函数值组成的集合也是
上的函数值组成的集合也是 ,若存在,求出
,若存在,求出 ,
, 的值;否则,说明理由.
的值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com