
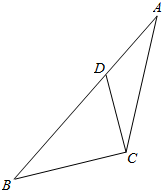
 如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.
如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.分析 (1)由$\overrightarrow{CB}$•$\overrightarrow{CD}$=0知∠BCD=90°,结合sin∠ACB=$\frac{5\sqrt{7}}{14}$可求出sin∠ACD,在△ACD中使用正弦定理求出∠ADC,∠A,和CD.
(2)∠B=∠ADC-∠BCD.
解答 解:(1)∵$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,∴∠BCD=90°.
∵sin∠ACB=sin(∠ACD+90°)=$\frac{5\sqrt{7}}{14}$,
∴cos∠ACD=$\frac{5\sqrt{7}}{14}$,∴sin∠ACD=$\frac{\sqrt{21}}{14}$.
在△ACD中,∵$\frac{AD}{sin∠ACD}=\frac{AC}{sin∠ADC}$,即$\frac{1}{\frac{\sqrt{21}}{14}}=\frac{\sqrt{7}}{sin∠ADC}$,
∴sin∠ADC=$\frac{\sqrt{3}}{2}$,∴∠ADC=120°.
∴∠A=60°-∠ACD,
∴sin∠A=sin(60°-∠ACD)=$\frac{\sqrt{3}}{2}×\frac{5\sqrt{7}}{14}-\frac{1}{2}×\frac{\sqrt{21}}{14}$=$\frac{\sqrt{21}}{7}$.
∵$\frac{CD}{sinA}=\frac{AD}{sin∠ACD}$,即$\frac{CD}{\frac{\sqrt{21}}{7}}=\frac{1}{\frac{\sqrt{21}}{14}}$,∴CD=2.
(2)∵∠B+∠BCD=∠ADC,
∴∠B=∠ADC-∠BCD=120°-90°=30°.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
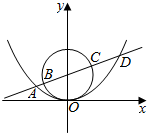 如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )
如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )| A. | 8p2 | B. | 4p2 | C. | 2p2 | D. | p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com