
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, ,若
,若 ,则
,则 ;若类比该命题,如图(2),三棱锥
;若类比该命题,如图(2),三棱锥 中,
中, 面
面 ,若
,若 点在三角形
点在三角形 所在平面内的射影为
所在平面内的射影为 ,则有什么结论?命题是否是真命题.
,则有什么结论?命题是否是真命题.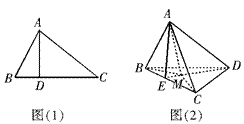
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
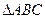 内一点,
内一点,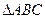 三边上的高分别为
三边上的高分别为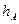 、
、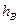 、
、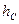 ,P到三边的距离依次为
,P到三边的距离依次为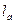 、
、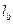 、
、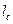 ,则有
,则有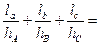 ______________;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是
______________;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是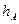 、
、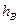 、
、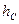 、
、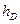 ,P到这四个面的距离依次是
,P到这四个面的距离依次是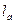 、
、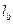 、
、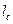 、
、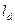 ,则有_________________。
,则有_________________。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
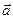 的性质
的性质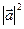 =
=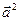 类比得到复数
类比得到复数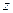 的性质
的性质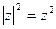 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,其中
,其中 为常数,等号右边的运算是通常意义的加乘运算,现已知
为常数,等号右边的运算是通常意义的加乘运算,现已知 ,
, ,且有一个非零实数m,使得对任意实数x,都有
,且有一个非零实数m,使得对任意实数x,都有 ,则
,则 ______________。
______________。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com