已知函数f(x)=x3-3ax2+b(a∈R,b∈R).
(I) 设a>0,求函数f(x)的单调区间;
(Ⅱ) 设a=-1,若方程f(x)=0在[-2,2]上有且仅有一个实数解,求b的取值范围.
解:( I)f'(x)=3x
2-6ax=3x(x-2a),…(2分)
因为a>0,所以2a>0
当x变化时,f(x),f'(x)的变化情况如下表:

当x>2a或x<0时,f'(x)>0;当0<x<2a时,f'(x)<0.
所以,当a>0时,函数f(x)的单调递增区间是(-∞,0)和(2a,+∞),
单调递减区间是(0,2a).…(6分)
( II)f(x)=x
3+3x
2+b,f'(x)=3x
2+6x=3x(x+2),x∈[-2,2]
当x变化时,f(x),f'(x)的变化情况如下表:
| x | -2 | (-2,0) | 0 | (0,2) | 2 |
| f'(x) | | - | 0 | + | |
| f(x) | b+4 | 递减 | 极小值b | 递增 | b+20 |
…(8分)
因为方程f(x)=0在区间[-2,2]有且仅有一个实数解,而b+4<b+20,
所以b=0,…(10分)
或
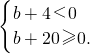
所以方程f(x)=0在区间[-2,2]有且仅有一个实数解时,b的取值范围是b=0或-20≤b<-4.…(12分)
分析:(I)先求导数fˊ(x)然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,fˊ(x)>0的区间为单调增区间,fˊ(x)<0的区间为单调减区间.
(II)由函数零点的存在定理,我们可以将区间[-2,2]分为区间(-2,0)和(0,2)两种情况进行分类讨论,最后综合讨论结果,即可得到f(x)=0在区间[-2,2]有且仅有一个实数解,则实数b的取值范围可得
点评:本题考查了函数的单调性、利用导数研究函数的极值,利用导数判断函数的单调性的步骤是:(1)确定函数的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.


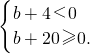


 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<