Question

已知二次函数f（x）=-3x²+2bx+c的图象经过原点，其对称轴方程为x=2．
（1）求函数f（x）的解析式；
（2）当x∈[2，3]时，求函数g（x）=f（x）-6（m+2）x-9的最大值h（m）．

Answer 1

解：（1）二次函数f（x）=-3x²+2bx+c的图象经过原点，则c=0，
又∵二次函数的图象对称轴是直线x=2，，
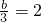
∴二次函数解析式为：y=-3x²+12x．
（2）g（x）=f（x）-6（m+2）x-9=-3x²-6mx-9，x∈[2，3]．
配方得，g（x）=-3（x+m）²+3m²-9，
∵m∈[-3，+∞），∴-m∈（-∞，3]
①当-m＜2时，m＞-2时，h（m）=g（2）=-12m-21；
②当2≤-m≤3时，-3≤m≤-2时，h（m）=g（-m）=3m²-9．
③当-m＞3时，m＜-3时，h（m）=g（3）=-36-18m．
综上，h（m）=．
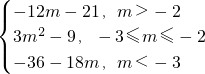
分析：（1）根据二次函数的图象经过原点，得c的值，根据图象对称轴是直线x=2，求出b值，从而得出解析式即可．
（2）根据二次函数的图象和性质，分别讨论函数的对称轴与区间[2，3]的关系，即可求出函数f（x）在[2，3]上的最大值h（m）的表达式；
点评：本题考查的是用待定系数法求二次函数的解析式，考查二次函数在闭区间上的最值，函数单调性的性质，二次函数的图象和性质，其中在解答含有参数的二次函数问题时，判断对称轴与给定区间的范围，以此为分类标准对参数进行分类讨论，是解答的关键．
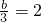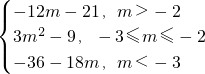