
【题目】如图所示三角形数阵中,aij为第i行第j个数,若amn=2017,则实数对(m,n)为 . 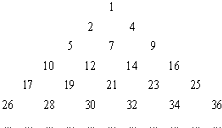
【答案】(45,41)
【解析】解:观察图象可发现以下规律:
(1)第一行有1个数字,第二行有2个数字,第三行有3个数字,…故可归纳得出第i行有i个数字;
(2)每一行的数字从左到右都是等差为2的等差数列;
(3)每一行的第一个数字都比上一行的最后一个数字大1;
(4)每一行的最后一个数字都是该行数的平方.
∵442=1936<2017,452=2025>2017,∴2017是第45行的数字,
设第45行第n个数字为an , 则a1=1937,d=2,∴an=1937+2(n﹣1)=2n+1935.
令an=2n+1935=2017,解得n=41.
∴2015是第45行第41个数字,
所以答案是(45,41).
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知{fn(x)}满足f1(x)= ![]() (x>0),fn+1(x)=f1[fn(x)],
(x>0),fn+1(x)=f1[fn(x)],
(1)求f2(x),f3(x),并猜想fn(x)的表达式;
(2)用数学归纳法证明对fn(x)的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合 计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合 计 | 60 | 50 | 110 |
根据上述数据能得出的结论是( )
(参考公式与数据:X2= ![]() .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
.当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
A.有99%的把握认为“爱好该项运动与性别有关”
B.有99%的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() +
+ ![]() +…+
+…+ ![]() =an﹣1(n∈N*),求数列{nbn}的前n项和Tn .
=an﹣1(n∈N*),求数列{nbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医院到某社区检查老年人的体质健康情况,从该社区全体老人中,随机抽取12名进行体质健康测试,测试成绩(百分制)如下:65,78,90,86,52,87,72,86,87,98,88,86.根据老年人体质健康标准,成绩不低于80的为优良.
(1)将频率视为概率,根据样本估计总体的思想,在该社区全体老年人中任选3人进行体质健康测试,求至少有1人成绩是“优良”的概率;
(2)从抽取的12人中随机选取3人,记ξ表示成绩“优良”的人数,求ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明. 下面是赵爽的弦图及注文,弦图是一个以勾股之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() 勾
勾![]() 股+(股-勾)
股+(股-勾)![]() 朱实+黄实=弦实,化简,得勾2+股2=弦2. 设勾股形中勾股比为
朱实+黄实=弦实,化简,得勾2+股2=弦2. 设勾股形中勾股比为![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. 134 B. 866 C. 300 D. 500
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com