
设函数![]()
![]() .
.
(1) 当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2) 当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值
上的最小值![]() 和最大值
和最大值![]() .
.
【解析】:![]()
(1)当![]() 时
时![]()
![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
(2)当![]() 时,
时,![]() ,其开口向上,对称轴
,其开口向上,对称轴![]() ,且过
,且过![]()
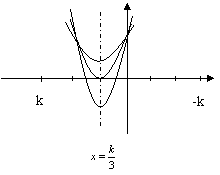 (i)当
(i)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
从而当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(ii)当![]() ,即
,即![]() 时,令
时,令![]()
解得:![]() ,注意到
,注意到![]() ,
,
(注:可用韦达定理判断![]() ,
,![]() ,从而
,从而![]() ;或者由对称结合图像判断)
;或者由对称结合图像判断)
![]()
![]()
![]() 的最小值
的最小值![]() ,
,
![]()
![]() 的最大值
的最大值![]()
综上所述,当![]() 时,
时,![]() 的最小值
的最小值![]() ,最大值
,最大值![]()
解法2(2)当![]() 时,对
时,对![]() ,都有
,都有![]() ,故
,故![]()
![]() 故
故![]() ,而
,而 ![]() ,
,![]()
所以 ![]() ,
,![]()
【解析】:看着容易,做着难!常规解法完成后,发现不用分类讨论,奇思妙解也出现了:结合图像感知![]() 时最小,
时最小,![]() 时最大,只需证
时最大,只需证![]() 即可,避免分类讨论.本题第二问关键在求最大值,需要因式分解比较深的功力,这也正符合了2012年高考年报的“对中学教学的要求——重视高一教学与初中课堂衔接课”.
即可,避免分类讨论.本题第二问关键在求最大值,需要因式分解比较深的功力,这也正符合了2012年高考年报的“对中学教学的要求——重视高一教学与初中课堂衔接课”.


科目:高中数学 来源: 题型:
| 1-x |
| x+3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com