
【题目】已知函数![]() ,
,![]()
![]() .
.
(1)求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求
时,求![]() 在
在![]() 上的最大值;
上的最大值;
(3)求证:![]() 的极大值小于1.
的极大值小于1.
【答案】(1)![]() ;(2)故当
;(2)故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)求出函数的导数,根据导数的几何意义求出切线斜率再由点斜式可得结果;(2)求出![]() 的解析式,求出
的解析式,求出![]() ,分别令
,分别令![]() 可得函数
可得函数![]() 增区间,令
增区间,令![]() 可得函数
可得函数![]() 的减区间,分类讨论,根据函数的单调性可求出
的减区间,分类讨论,根据函数的单调性可求出![]() 的最大值;(3)求出函数的导数
的最大值;(3)求出函数的导数![]() ,两次求导可判断函数的单调性,利用单调性求出函数的极值,判断即可.
,两次求导可判断函数的单调性,利用单调性求出函数的极值,判断即可.
(1)∵![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ,
,
(2)![]() ,(
,(![]() ),令
),令![]() ,得
,得![]() ,
,
在区间![]() 上,
上,![]() ,函数
,函数![]() 是增函数;
是增函数;
在区间![]() 上,
上,![]() ,函数
,函数![]() 是减函数;
是减函数;
故当![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() .
.
当![]() 时,
时,![]() 先增后减,故
先增后减,故![]() .
.
当![]() 时,
时,![]() 在
在![]() 上递增,此时
上递增,此时![]() .
.
(3)![]() ,令
,令![]() ,
,
![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,所以存在唯一的
,所以存在唯一的![]() ,
,
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,其中
,其中![]() ,所以函数
,所以函数![]() 有极大值.
有极大值.
函数![]() 的极大值是
的极大值是![]() ,由
,由![]() ,得
,得![]() ,
,
所以 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 的极大值小于1.
的极大值小于1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:
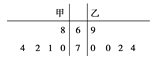
计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国明代商人程大位对文学和数学也颇感兴趣,他于60岁时完成杰作![]() 直指算法统宗
直指算法统宗![]() ,这是一本风行东亚的数学名著,该书第五卷有问题云:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”翻译成现代文就是:“今有百米一百八十石,甲乙丙三个人来分,他们分得的米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少米?”请你计算甲应该分得
,这是一本风行东亚的数学名著,该书第五卷有问题云:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”翻译成现代文就是:“今有百米一百八十石,甲乙丙三个人来分,他们分得的米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少米?”请你计算甲应该分得![]()
![]()
A. 78石 B. 76石 C. 75石 D. 74石
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】摩拜单车和![]() 小黄车等各种共享单车的普及给我们的生活带来了便利.已知某共享单车的收费标准是:每车使用不超过1小时(包含1小时)是免费的,超过1小时的部分每小时收费1元(不足1小时的部分按1小时计算,例如:骑行2.5小时收费2元).现有甲、乙两人各自使用该种共享单车一次.设甲、乙不超过1小时还车的概率分别为
小黄车等各种共享单车的普及给我们的生活带来了便利.已知某共享单车的收费标准是:每车使用不超过1小时(包含1小时)是免费的,超过1小时的部分每小时收费1元(不足1小时的部分按1小时计算,例如:骑行2.5小时收费2元).现有甲、乙两人各自使用该种共享单车一次.设甲、乙不超过1小时还车的概率分别为![]() 1小时以上且不超过2小时还车的概率分别为
1小时以上且不超过2小时还车的概率分别为![]() 两人用车时间都不会超过3小时.
两人用车时间都不会超过3小时.
(Ⅰ)求甲乙两人所付的车费相同的概率;
(Ⅱ)设甲乙两人所付的车费之和为随机变量![]() 求
求![]() 的分布列及数学期望
的分布列及数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,
,![]() .
.
(1)直线![]() 是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
(2)已知点![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 满足条件
满足条件![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于![]() 到
到![]() 之间,将数据分成以下
之间,将数据分成以下![]() 组:第
组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第
,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第![]() ,
, ![]() ,
, ![]() 组中随机抽取
组中随机抽取![]() 名学生做初检.
名学生做初检.
(![]() )求每组抽取的学生人数.
)求每组抽取的学生人数.
(![]() )若从
)若从![]() 名学生中再次随机抽取
名学生中再次随机抽取![]() 名学生进行复检,求这
名学生进行复检,求这![]() 名学生不在同一组的概率.
名学生不在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由一平面内的
是由一平面内的![]() 个向量组成的集合.若
个向量组成的集合.若![]() ,且
,且![]() 的模不小于
的模不小于![]() 中除
中除![]() 外的所有向量和的模.则称
外的所有向量和的模.则称![]() 是
是![]() 的极大向量.有下列命题:
的极大向量.有下列命题:
①若![]() 中每个向量的方向都相同,则
中每个向量的方向都相同,则![]() 中必存在一个极大向量;
中必存在一个极大向量;
②给定平面内两个不共线向量![]() ,在该平面内总存在唯一的平面向量
,在该平面内总存在唯一的平面向量![]() ,使得
,使得![]() 中的每个元素都是极大向量;
中的每个元素都是极大向量;
③若![]() 中的每个元素都是极大向量,且
中的每个元素都是极大向量,且![]() 中无公共元素,则
中无公共元素,则![]() 中的每一个元素也都是极大向量.
中的每一个元素也都是极大向量.
其中真命题的序号是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com