
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
科目:高中数学 来源:不详 题型:填空题
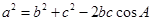 ,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B, V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为
,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B, V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为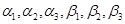 我们可以得到“四面体的余弦定理”:_____________________.(只需写出一个关系式)
我们可以得到“四面体的余弦定理”:_____________________.(只需写出一个关系式)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.两条直线平行,同旁内角互补;如果 和 和 是两条直线平行的同旁内角,则 是两条直线平行的同旁内角,则 + + = = 。 。 |
| B.由平面三角形的性质,推测空间四面体的性质。 |
| C.某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人。 |
D.在数列 中, 中,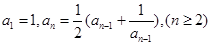 ,由 ,由 推测 推测 的通项公式。 的通项公式。 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 .根
.根 据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为
据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为 ,内切球的半径为r,则四面体的体积为( )
,内切球的半径为r,则四面体的体积为( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com