
【题目】甲、乙两名射击运动员在进行射击训练,已知甲命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,乙命中10环,9环,8环的概率分别是
,乙命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,任意两次射击相互独立.
,任意两次射击相互独立.
(1)求甲运动员两次射击命中环数之和恰好为18的概率;
(2)现在甲、乙两人进行射击比赛,每一轮比赛两人各射击1次,环数高于对方为胜,环数低于对方为负,环数相等为平局,规定连续胜利两轮的选手为最终的胜者,比赛结束,求恰好进行3轮射击后比赛结束的概率
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)甲运动员两次射击命中环数之和恰好为18包含“第一次10环和第二次8环”,“第一次8环第二次10环”,“第一次9环和第二次9环”这三种情况,分别求三种情况概率再求和;
(2)求恰好进行3轮射击后比赛结束的概率,先确定甲胜利,平局,失败的概率,恰好进行3轮射击后比赛结束情形包括两种:①当甲获得最终胜利结束3轮比赛时,由第2轮、第3轮甲连续胜利,第一轮甲没有获得胜利,算出其概率P1![]() ;②当乙获得最终胜利结束3轮比赛时,则第2轮、第3轮乙连续胜利,第1轮乙没有获得胜利,其概率P2
;②当乙获得最终胜利结束3轮比赛时,则第2轮、第3轮乙连续胜利,第1轮乙没有获得胜利,其概率P2![]() ,两情形概率之和即为所求.
,两情形概率之和即为所求.
(1)记X表示甲运动员两次射击命中环数之和,
则X=18包含“第一次10环和第二次8环”,“第一次8环第二次10环”,“第一次9环和第二次9环”这三种情况,
∴甲运动员两次射击命中环数之和恰好为18的概率为:
P![]() .
.
(2)记Ai表示甲在第i轮胜利,Bi表示甲在第i轮平局,i表示甲在第i轮失败,
∴P(Ai)![]() ,P(Bi)
,P(Bi)![]() ,P(i)
,P(i)![]() ,
,
①当甲获得最终胜利结束3轮比赛时,由第2轮、第3轮甲连续胜利,第一轮甲没有获得胜利,
其概率P1![]() ,
,
②当乙获得最终胜利结束3轮比赛时,则第2轮、第3轮乙连续胜利,第1轮乙没有获得胜利,
其概率P2![]() ,
,
∴经过3轮比赛结束的概率P![]() .
.


科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
![]() ,
,
(1)求![]()
![]()
![]() 的值,并求出
的值,并求出![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)设![]() 求数列
求数列![]() 的前n项和
的前n项和![]()
(3)设![]()
![]() 在数列
在数列![]() 中取出
中取出![]() (
(![]() 为常数)项,按照原来的顺序排成一列,构成等比数列
为常数)项,按照原来的顺序排成一列,构成等比数列![]() .若对任意的数列
.若对任意的数列![]() ,均有
,均有![]() 试求
试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当点![]() 在椭圆
在椭圆![]() 的图像上运动时,点
的图像上运动时,点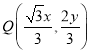 在曲线
在曲线![]() 上运动,求曲线
上运动,求曲线![]() 的轨迹方程,并指出该曲线是什么图形;
的轨迹方程,并指出该曲线是什么图形;
(3)过椭圆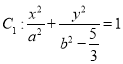 上异于其顶点的任意一点
上异于其顶点的任意一点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在
在![]() 轴,
轴,![]() 轴上的截距分别为
轴上的截距分别为![]() 试问:
试问:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数为F(x) .有下列四个命题:①此函数为偶函数,且有无数条对称轴;②此函数的值域是
.有下列四个命题:①此函数为偶函数,且有无数条对称轴;②此函数的值域是![]() ;③此函数为周期函数,但没有最小正周期;④存在三点
;③此函数为周期函数,但没有最小正周期;④存在三点![]() ,使得△ABC是等腰直角三角形,以上命题正确的是( )
,使得△ABC是等腰直角三角形,以上命题正确的是( )
A.①②B.①③C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列![]() 的前n项和为
的前n项和为![]() 且满足
且满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 求正整数
求正整数![]() 的值;
的值;
(3)是否存在正整数![]() ,使得
,使得![]() 恰好为数列
恰好为数列![]() 的一项?若存在,求出所有满足条件的正整数
的一项?若存在,求出所有满足条件的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com