已知顶点在原点、焦点F在y轴正半轴上的抛物线Q1过点(2,1),抛物线Q2与Q1关于x轴对称.
(I)求抛物线Q2的方程;
(II)过点F的直线交抛物线Q1于点A(x1,y1),B(x2,y2)(x1<x2),过A、B分别作Q1的切线l1,l2,记直线l1与Q2的交点为M(m1,n1),N(m2,n2)(m1<m2),求证:抛物线Q2上的点S(s,t)若满足条件m2s=4,则S恰在直线l2上.
解:(I)设抛物线Q
1方程为x
2=2py(p>0),
依题意知4=2p∴p=2.
∴Q
1:x
2=4y
又∵抛物线Q
2与Q
1关于x轴对称
∴抛物线Q
2的方程为:x
2=-4y.
(II)由题意知AB 的斜率存在,且过焦点(0,1),所以设直线方程为:y=kx+1.
联立
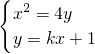
消y得:x
2-4kx-4=0.则x
1x
2=-4.
∵抛物线Q
1的方程为x
2=4y,即y=
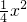
.
∴y′=

x,则直线l
1的方程为y-y
1=
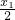
(x-x
1)
又y
1=
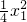
∴直线l
1的方程为y=
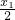
x-
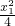
同理可得直线l
2的方程为y=
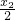
x-
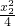
∵N(m
2,n
2)在直线l
1上,且n
2=-
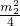
∴
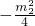
=
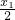
m
2-
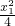
①.
又∵x
1x
2=-4,m
2s=4∴x
1=-
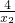
,m
2=
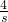
则代入①式得:
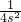
=
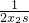
+
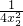
两边同乘以s
2x
22,得
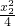
=
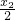
s+
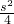
,即-
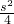
=
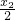
s-
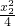
而t=-
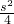
,∴t=
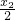
s-
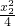
,即点S(s,t)满足直线l
2的方程.
故点S恰在直线l
2上.
分析:(I)设出抛物线Q
1对应的标准方程,代入点(2,1),则求得抛物线Q
1的方程;然后根据抛物线Q
2与Q
1关于x轴对称,则焦点关于x轴对称,开口方向相反,显然易得抛物线Q
2的方程.
(II)先设出直线AB的方程;然后与抛物线Q
1联立方程组并消y,得关于x的一元二次方程,并由韦达定理表示出x
1x
2的值;再根据直线l
1、l
2是抛物线Q
1的切线,则通过导数求其斜率,进而表示出l
1、l
2的方程;由于点S(s,t)的横坐标s与m
2有等量关系m
2s=4,则从点N(m
2,n
2)入手,把n
2用m
2的代数式替换,并根据点N在直线l
1上建立等量关系式;再根据
x
1x
2=-4用x
2替换x
1,经变形使刚才的等式与直线l
2的方程形式更加接近;最后由点S(s,t)在Q
2上,满足t=-
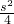
,则代入形如l
2方程的等式,使点S(s,t)的坐标s、t恰好满足直线l
2的方程.则问题解决.
点评:直线与圆锥曲线的相交问题,一般需联立方程组,并消元得一元二次方程,进而利用韦达定理来处理;再者,要证明点恒在线上,需始终明确目标(即欲证点的坐标满足直线方程),从相对复杂的关系中不断变形,最终到达目的地.

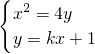 消y得:x2-4kx-4=0.则x1x2=-4.
消y得:x2-4kx-4=0.则x1x2=-4.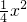 .
. x,则直线l1的方程为y-y1=
x,则直线l1的方程为y-y1=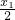 (x-x1)
(x-x1)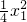 ∴直线l1的方程为y=
∴直线l1的方程为y=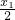 x-
x-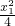
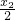 x-
x-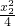
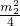
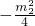 =
=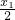 m2-
m2-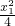 ①.
①.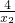 ,m2=
,m2=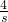
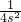 =
=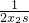 +
+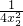
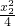 =
=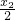 s+
s+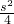 ,即-
,即-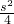 =
=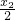 s-
s-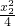
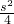 ,∴t=
,∴t=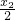 s-
s-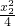 ,即点S(s,t)满足直线l2的方程.
,即点S(s,t)满足直线l2的方程.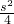 ,则代入形如l2方程的等式,使点S(s,t)的坐标s、t恰好满足直线l2的方程.则问题解决.
,则代入形如l2方程的等式,使点S(s,t)的坐标s、t恰好满足直线l2的方程.则问题解决.
